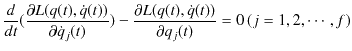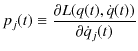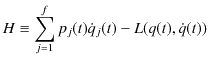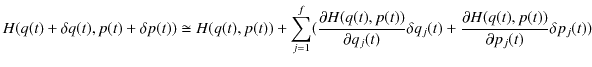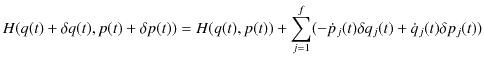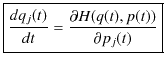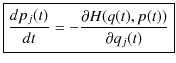Chapter2 ハミルトニアン形式

2.1 一般化運動量

このChapterでは，解析力学のもう1つの形式であるハミルトニアン形式を取り扱います．"ラグランジアン形式" のChapterより，ラグランジアンは $ 2f$ 個の変数の関数でした．（$ f$ は自由度で，$ N$ 粒子系の場合は $ f=3N$ です．）

$\displaystyle L=L(q_{1}(t),q_{2}(t),\cdots,q_{f}(t),\dot{q}_{1}(t),\dot{q}_{2}(t),\cdots,\dot{q}_{f}(t))=L(q(t),\dot{q}(t))$

最右辺の式は，変数を簡略化して表したものです．ラグランジアンはオイラー-ラグランジュ方程式，

$\displaystyle \dfrac{d}{dt}(\dfrac{\partial L(q(t),\dot{q}(t))}{\partial\dot{q}... ...t)})-\dfrac{\partial L(q(t),\dot{q}(t))}{\partial q_{j}(t)}=0\,(j=1,2,\cdots,f)$ (2.1)

を満たします．このオイラー-ラグランジュ方程式(2.1)式の中にも現れる次の量を，一般化運動量 $ p_{j}(t)\,(j=1,2,\cdots,f)$ として定義します．

$\displaystyle p_{j}(t)\equiv\dfrac{\partial L(q(t),\dot{q}(t))}{\partial\dot{q}_{j}(t)}$ (2.2)

　デカルト座標の場合，この一般化運動量が通常の意味での運動量と一致することを確認しておきましょう．運動エネルギーを $ T(\dot{\bm{x}}(t))$，ポテンシャルを $ V(\bm{x}(t))$ として，1質点のラグランジアン $ L(\bm{x}(t),\dot{\bm{x}}(t))=T(\dot{\bm{x}}(t))-V(\bm{x}(t))$ は，

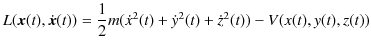
$\displaystyle L(\bm{x}(t),\dot{\bm{x}}(t))=\dfrac{1}{2}m(\dot{x}^{2}(t)+\dot{y}^{2}(t)+\dot{z}^{2}(t))-V(x(t),y(t),z(t))$

ですから，(2.2)式より，機械的に $ x(t)$ 成分の一般化運動量を計算すると，

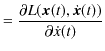$\displaystyle p_{x}(t)$ $\displaystyle =\dfrac{\partial L(\bm{x}(t),\dot{\bm{x}}(t))}{\partial\dot{x}(t)}$    
  $\displaystyle =m\dot{x}(t)$    

となり，確かに通常の運動量になりますね．$ y(t)$ 成分と $ z(t)$ 成分についても同様です．

 

2.2 ハミルトニアン

系を記述する物理量として，全力学的エネルギー，

$\displaystyle H\equiv T+V$

を，ハミルトニアン $ H$ として定義します．ここで，$ T$ は運動エネルギー，$ V$ はポテンシャルです．さらに，一般化してハミルトニアン $ H$ を，

$\displaystyle H\equiv\sum_{j=1}^{f}p_{j}(t)\dot{q}_{j}(t)-L(q(t),\dot{q}(t))$ (2.3)

と定義しなおします．特別に，1質点についてデカルト座標を考えると，

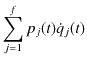$\displaystyle \sum_{j=1}^{f}p_{j}(t)\dot{q}_{j}(t)$ $\displaystyle =m\dot{x}^{2}(t)+m\dot{y}^{2}(t)+m\dot{z}^{2}(t)$    
  $\displaystyle =2T(q(t),\dot{q}(t))$    

となりますので，確かに，

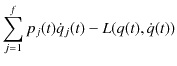$\displaystyle \sum_{j=1}^{f}p_{j}(t)\dot{q}_{j}(t)-L(q(t),\dot{q}(t))$ $\displaystyle =2T(q(t),\dot{q}(t))-(T(q(t),\dot{q}(t))-V(q(t)))$    
  $\displaystyle =T(q(t),\dot{q}(t))+V(q(t))$    

であることがわかります．(2.3)式のハミルトニアンの定義は，1質点についてデカルト座標の場合を含んでいることがわかります．(2.3)式が，最も一般的なハミルトニアンの定義式です．

　ハミルトニアン(2.3)式の右辺は， $ q_{1}(t),q_{2}(t),\cdots,q_{f}(t),\dot{q}_{1}(t),\dot{q}_{2}(t),\cdots,\dot{q}_{f}(t)$ と， $ p_{1}(t),p_{2}(t),\cdots,p_{f}(t)$ の変数からなりますが，ここで，(2.2)式の関係より， $ \dot{q}_{1}(t),\dot{q}_{2}(t),\cdots,\dot{q}_{f}(t)$ を $ p_{1}(t),p_{2}(t),\cdots,p_{f}(t)$ で表すことにします．このとき，ハミルトニアン $ H$ は， $ q_{1}(t),q_{2}(t),\cdots,q_{f}(t),p_{1}(t),p_{2}(t),\cdots,p_{f}(t)$ の $ 2f$ 個の変数をもちます．すなわち，

$\displaystyle H=H(q_{1}(t),q_{2}(t),\cdots,q_{f}(t),p_{1}(t),p_{2}(t),\cdots,p_{f}(t))=H(q(t),p(t))$

です．最右辺の式は，変数を簡略化して書いたものです．独立した $ 2f$ 個の変数，

$\displaystyle q_{1}(t),q_{2}(t),\cdots,q_{f}(t),p_{1}(t),p_{2}(t),\cdots,p_{f}(t)$

を正準変数といいます．

 

2.3 ハミルトン正準方程式

ハミルトニアンの満たす運動方程式を導出しましょう．いま，正準変数 $ q_{j}(t),p_{j}(t)$ について変分をとります．すなわち，

  $\displaystyle q_{j}(t)\to q_{j}(t)+\delta q_{j}(t)$    
  $\displaystyle p_{j}(t)\to p_{j}(t)+\delta p_{j}(t)$    

とします．このとき， $ \dot{q}_{j}(t)$ は $ q_{j}(t),p_{j}(t)$ の関数になりますので，2次の変分を無視して，

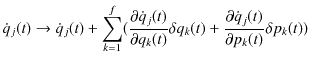
$\displaystyle \dot{q}_{j}(t)\to\dot{q}_{j}(t)+\sum_{k=1}^{f}(\dfrac{\partial\do... ...elta q_{k}(t)+\dfrac{\partial\dot{q}_{j}(t)}{\partial p_{k}(t)}\delta p_{k}(t))$

のように変化します．さて，ハミルトニアンについては，2次の変分を無視して，

$\displaystyle H(q(t)+\delta q(t),p(t)+\delta p(t))\cong H(q(t),p(t))+\sum_{j=1}... ...delta q_{j}(t)+\dfrac{\partial H(q(t),p(t))}{\partial p_{j}(t)}\delta p_{j}(t))$ (2.4)

となります．一方，ハミルトニアンの定義(2.3)式より，

$\displaystyle H(q(t)+\delta q(t),p(t)+\delta p(t))$ $\displaystyle \cong\sum_{j=1}^{f}[(p_{j}(t)+\delta p_{j}(t))\{\dot{q}_{j}(t)+\s... ...partial\dot{q}_{j}(t)}{\partial p_{k}(t)}\delta p_{k}(t))\}]-L(q(t),\dot{q}(t))$    
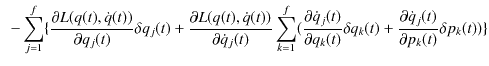  $\displaystyle \,\,\,-\sum_{j=1}^{f}\{\dfrac{\partial L(q(t),\dot{q}(t))}{\parti... ...ta q_{k}(t)+\dfrac{\partial\dot{q}_{j}(t)}{\partial p_{k}(t)}\delta p_{k}(t))\}$    
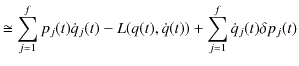  $\displaystyle \cong\sum_{j=1}^{f}p_{j}(t)\dot{q}_{j}(t)-L(q(t),\dot{q}(t))+\sum_{j=1}^{f}\dot{q}_{j}(t)\delta p_{j}(t)$    
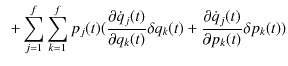  $\displaystyle \,\,\,+\sum_{j=1}^{f}\sum_{k=1}^{f}p_{j}(t)(\dfrac{\partial\dot{q... ...elta q_{k}(t)+\dfrac{\partial\dot{q}_{j}(t)}{\partial p_{k}(t)}\delta p_{k}(t))$    
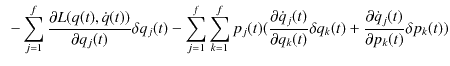  $\displaystyle \,\,\,-\sum_{j=1}^{f}\dfrac{\partial L(q(t),\dot{q}(t))}{\partial... ...elta q_{k}(t)+\dfrac{\partial\dot{q}_{j}(t)}{\partial p_{k}(t)}\delta p_{k}(t))$    

最後の変形においては，2次の変分を無視し，一般化運動量の定義(2.2)を使いました．さらに，計算を続けます．

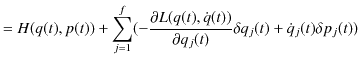$\displaystyle H(q(t)+\delta q(t),p(t)+\delta p(t))$ $\displaystyle =H(q(t),p(t))+\sum_{j=1}^{f}(-\dfrac{\partial L(q(t),\dot{q}(t))}{\partial q_{j}(t)}\delta q_{j}(t)+\dot{q}_{j}(t)\delta p_{j}(t))$    
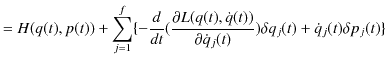  $\displaystyle =H(q(t),p(t))+\sum_{j=1}^{f}\{-\dfrac{d}{dt}(\dfrac{\partial L(q(... ...q}(t))}{\partial\dot{q}_{j}(t)})\delta q_{j}(t)+\dot{q}_{j}(t)\delta p_{j}(t)\}$    

ですから，

$\displaystyle H(q(t)+\delta q(t),p(t)+\delta p(t))=H(q(t),p(t))+\sum_{j=1}^{f}(-\dot{p}_{j}(t)\delta q_{j}(t)+\dot{q}_{j}(t)\delta p_{j}(t))$ (2.5)

となります．ここで，ハミルトニアンの定義式(2.3)式，オイラー-ラグランジュ方程式(2.1)式と，一般化運動量の定義(2.2)式を使いました．(2.4)式と(2.5)式を比較して，

$\displaystyle \fbox{$\dfrac{dq_{j}(t)}{dt}=\dfrac{\partial H(q(t),p(t))}{\partial p_{j}(t)}$}$ (2.6)

と，

$\displaystyle \fbox{$\dfrac{dp_{j}(t)}{dt}=-\dfrac{\partial H(q(t),p(t))}{\partial q_{j}(t)}$}$ (2.7)

を得ます．(2.6)式と(2.7)式をハミルトン正準方程式といいます．ハミルトニアン形式で中心的な働きをする方程式です．

　ここで，1質点の場合，確かにハミルトン正準方程式からニュートンの運動方程式が導かれることを確認しておきましょう．一般化座標としてデカルト座標 $ \bm{x}=(x(t),y(t),z(t))$ をとり，質点の質量を $ m$，ポテンシャルを $ V(\bm{x}(t))$ とします．このとき，ハミルトニアン $ H(\bm{x}(t),\bm{p}(t))=T(\bm{p}(t))+V(\bm{x}(t))$ は，

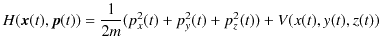
$\displaystyle H(\bm{x}(t),\bm{p}(t))=\dfrac{1}{2m}(p_{x}^{2}(t)+p_{y}^{2}(t)+p_{z}^{2}(t))+V(x(t),y(t),z(t))$

で与えられます．（座標と運動量でハミルトニアンを記述していることに注意します．）$ x(t)$成分について調べると，ハミルトン正準方程式の第1式，(2.6)式より，

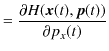$\displaystyle \dfrac{dx(t)}{dt}$ $\displaystyle =\dfrac{\partial H(\bm{x}(t),\bm{p}(t))}{\partial p_{x}(t)}$    
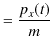  $\displaystyle =\dfrac{p_{x}(t)}{m}$    

となります．この式は運動量の定義式と一致します．また，ハミルトン正準方程式の第2式，(2.7)式より，

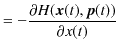$\displaystyle \dfrac{dp_{x}(t)}{dt}$ $\displaystyle =-\dfrac{\partial H(\bm{x}(t),\bm{p}(t))}{\partial x(t)}$    
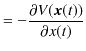  $\displaystyle =-\dfrac{\partial V(\bm{x}(t))}{\partial x(t)}$    

となります．よって，

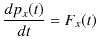
$\displaystyle \dfrac{dp_{x}(t)}{dt}=F_{x}(t)$

となり，ニュートンの運動方程式が再現されることが確認されました．$ y(t)$ 成分と $ z(t)$ 成分についても同様です．