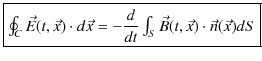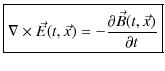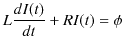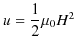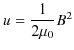Chapter11 電磁誘導(ファラデーの法則)
11.1 ファラデーの電磁誘導の法則
磁石をコイルに近づけたり遠ざけたりすると,コイルに電流が流れます.この現象を電磁誘導といいます.電磁誘導による起電力を誘導起電力,その電流を誘導電流といいます.電磁誘導を取り扱うために,新しく磁束 ![]() という物理量を次式で定義します.
という物理量を次式で定義します.
定義11.1(磁束1)
![]()
直観的に磁束とは,磁場を束ねた物理量です.ここで,![]() は磁束密度,
は磁束密度,![]() は磁束密度に垂直な断面積を表します.この式から磁束密度という名前の由来がわかると思います.つまり,
は磁束密度に垂直な断面積を表します.この式から磁束密度という名前の由来がわかると思います.つまり,![]() は,単位面積当たりの磁束になっています.また,
は,単位面積当たりの磁束になっています.また,
![]() の関係があります.電磁誘導を磁束という言葉で言い直すと,
の関係があります.電磁誘導を磁束という言葉で言い直すと,
"磁束が変化すると誘導起電力が発生します."
と表現されます.また,誘導起電力の向きに関しては,
法則11.1(レンツの法則) "誘導電流は,磁束の変化を妨げる向きに流れます."
というレンツの法則が成立します.図を見て下さい.最も簡単な電磁誘導の例を挙げています.
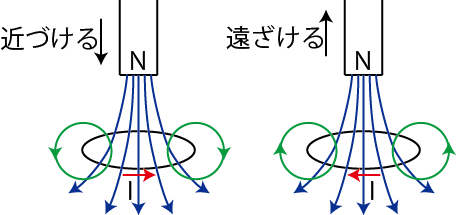
Figure11.1: 電磁誘導1
図の青い線が磁石の磁束密度を表し,緑の線が誘導電流による磁束密度を表しています.左側の例では磁石を近づけると磁束密度が強くなり,下向きの磁束が増加します.それを妨げるため上向きの磁束が生じるように誘導電流が流れます.親指が,生じる磁束の向きと同じ,上向きになるようにして右手でコイルを握り,中指の向きの誘導電流が流れることになります.右側の例では磁石を遠ざけると磁束密度が弱くなり,下向きの磁束が減少します.それを妨げるため下向きの磁束が生じるように誘導電流が流れます.親指が,生じる磁束の向きと同じ,下向きになるようにして右手でコイルを握り,中指の向きの誘導電流が流れることになります.誘導起電力の大きさに関しては,
法則11.2(ファラデーの電磁誘導の法則) "誘導起電力の大きさは,磁束の単位時間当たりの変化量に比例します."
というファラデーの電磁誘導の法則が成立します.誘導起電力の向きと大きさを次式で表します.
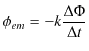
ここで,![]() は比例定数であり,正の値をとります.また,右辺の負符号はレンツの法則,つまり磁束の変化と妨げるように誘導起電力が生じることを示しています.
は比例定数であり,正の値をとります.また,右辺の負符号はレンツの法則,つまり磁束の変化と妨げるように誘導起電力が生じることを示しています.
![]() を限りなく 0 に近づける極限をとると,ファラデーの電磁誘導の法則は次式になります.
を限りなく 0 に近づける極限をとると,ファラデーの電磁誘導の法則は次式になります.
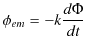
電磁誘導の典型的な次の例として,磁場中で動く導体棒を取り上げましょう.上の磁石が動く例では,磁束密度 ![]() が変わり磁束が変化しました.すなわち,
が変わり磁束が変化しました.すなわち,
でした.今度の磁場中で動く導体棒の場合は,磁束密度は一定ですが回路の面積 ![]() が変わり磁束が変化します.この場合は,
が変わり磁束が変化します.この場合は,
の関係になります.磁場中を動く導体棒の状況は図の通りです.
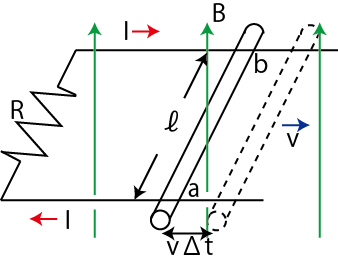
Figure11.2: 電磁誘導2
一様な磁束密度 ![]() が上向きにかかっていて,その中を長さ
が上向きにかかっていて,その中を長さ ![]() の導体棒が速さ
の導体棒が速さ ![]() で右向きに引っ張られて運動しています.このとき,
で右向きに引っ張られて運動しています.このとき,
![]() の間に回路の面積が,
の間に回路の面積が,
だけ増すので,回路を貫く磁束は上向きに,
だけ増加します.レンツの法則より,磁束の変化を妨げるように下向きの磁束が生じるように誘導電流が流れます.右手で回路を握り,親指を下にすると中指の向きが誘導電流の向きになります.したがって,導体棒中では図の ![]() から
から ![]() の向きへ誘導電流が流れます.この場合,導体棒は電池の役目をしているので,静電位は
の向きへ誘導電流が流れます.この場合,導体棒は電池の役目をしているので,静電位は ![]() の方が
の方が ![]() よりも高くなります.これは,導体棒中で静電位が低い
よりも高くなります.これは,導体棒中で静電位が低い ![]() から静電位の高い
から静電位の高い ![]() へ,エネルギーを与え,電流を押し流していることを意味します.ファラデーの電磁誘導の法則,
へ,エネルギーを与え,電流を押し流していることを意味します.ファラデーの電磁誘導の法則,
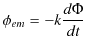
より,誘導起電力は,
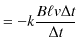 |
||
となります.負符号は誘導起電力の向きを表すので,その大きさは,
となります.
同じ現象をローレンツ力によっても説明できることを見ておきましょう.図のように1本の導体棒が単独で上向きの一様な磁束密度 ![]() の中を動いています.
の中を動いています.
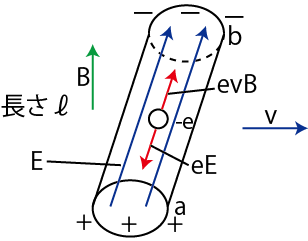
Figure11.3: 電磁誘導3
棒の中には電流の担い手としての自由電子があり,これが棒とともに動いているので,電子は磁束密度からローレンツ力を受けます.電子の電荷を ![]() として,1個の電子が受けるローレンツ力を求めましょう.負の電荷をもつ電子が右に動いているので,電流が左に流れていると考えることができます.フレミングの左手の法則より,ローレンツ力の向きは
として,1個の電子が受けるローレンツ力を求めましょう.負の電荷をもつ電子が右に動いているので,電流が左に流れていると考えることができます.フレミングの左手の法則より,ローレンツ力の向きは ![]() から
から ![]() の向きです.そして,その大きさは
の向きです.そして,その大きさは ![]() で与えられます.この力を受けて電子が移動するため,
で与えられます.この力を受けて電子が移動するため,![]() 端では電子が過剰になって負に,
端では電子が過剰になって負に,![]() 端では電子が不足して正に帯電し,棒の中には
端では電子が不足して正に帯電し,棒の中には ![]() から
から ![]() の向きに電場が生じます.この電場の強さを
の向きに電場が生じます.この電場の強さを ![]() とすると,電子は
とすると,電子は ![]() から
から ![]() の向きに
の向きに ![]() のクーロン力を受けます.ここで,電流は一定に流れるので,電子は等速運動をしています.したがって,慣性の法則より,ローレンツ力とクーロン力はつりあうので,
のクーロン力を受けます.ここで,電流は一定に流れるので,電子は等速運動をしています.したがって,慣性の法則より,ローレンツ力とクーロン力はつりあうので,
となります.故に,![]() 間の電位差は,
間の電位差は,
![]() より,
より,
すなわち,
となります.これが誘導起電力になります.(11.1)式と(11.2)式を比較すると,![]() となることがわかります.故に,ファラデーの電磁誘導の法則は,
となることがわかります.故に,ファラデーの電磁誘導の法則は,
となることが理解されます.実はそれだけではなく,ファラデーの電磁誘導の法則の磁束の磁束密度 ![]() と,ローレンツ力の磁束密度
と,ローレンツ力の磁束密度 ![]() が同一のものであることが,ここで判明するのです.これは重要な理論的事実です.
が同一のものであることが,ここで判明するのです.これは重要な理論的事実です.
この磁場中で動く導体棒について,エネルギー保存則の関係が成立することも見ておきましょう.状況は図の通りです.
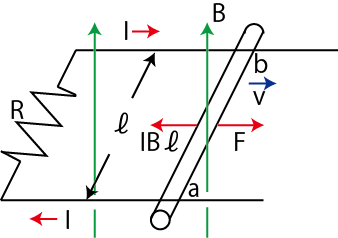
Figure11.4: エネルギー保存則
力関係は,外力 ![]() と誘導電流によるアンペール力
と誘導電流によるアンペール力 ![]() (フレミングの左手の法則より,この場合左向き.)がつりあっています.つまり,
(フレミングの左手の法則より,この場合左向き.)がつりあっています.つまり,
です.ここで,外力がする仕事率 ![]() は,
は,![]() より,
より,
となります.これは,外力がした仕事の分だけ,抵抗でジュール熱が発生していることを表しています.つまり,エネルギー保存則が成立していることがわかります.もちろん,エネルギー保存則は,この磁場中で動く導体棒の例だけでなく,電磁誘導の現象一般に成立します.
ファラデーの電磁誘導の法則を一般化しておきましょう.磁束 ![]() は,磁束密度と断面積が垂直でない場合と磁束密度が一様でない場合も含めて,次の式で定義されます.
は,磁束密度と断面積が垂直でない場合と磁束密度が一様でない場合も含めて,次の式で定義されます.
定義11.2(磁束2)
![]()
ただし,
![]() は法線ベクトルです.また,起電力
は法線ベクトルです.また,起電力 ![]() は電場が回路
は電場が回路 ![]() の1周にわたって単位電荷になす仕事なので,
の1周にわたって単位電荷になす仕事なので,
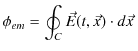
となります.したがって,(11.3)式,
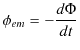
は,
となります.この(11.4)式をファラデーの電磁誘導の法則(積分形)といいます.ここで,ベクトル解析のストークスの定理,
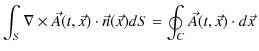
より,(11.4)式は,
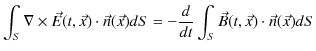
となります.ここで,両辺の被積分関数が等しいので,
が成立します.(11.5)式をファラデーの電磁誘導の法則(微分形)といいます.
11.2 自己誘導
一つのコイルに流れる電流が変化すると,この電流によってつくられていた磁場が変化して,このコイルを貫く磁束が変わります.このために,このコイルの中に誘導起電力が発生します.この現象を自己誘導といいます.コイルの電流を ![]() とし,
とし,![]() のためにコイルを貫く磁束を
のためにコイルを貫く磁束を ![]() とすれば,
とすれば,![]() は
は ![]() に比例します.ここで,比例定数を
に比例します.ここで,比例定数を ![]() (ヘンリー)とすると,
(ヘンリー)とすると,
の関係が成立します.![]() のことを自己インダクタンスといいます.電流
のことを自己インダクタンスといいます.電流 ![]() が減少するとき,磁束
が減少するとき,磁束 ![]() も減少するので,レンツの法則より,電流
も減少するので,レンツの法則より,電流 ![]() を減らさない向きに誘導起電力が発生します.逆に,コイルの電流
を減らさない向きに誘導起電力が発生します.逆に,コイルの電流 ![]() が増加するときには,それを増やさない向きに起電力がコイルに生じます.自己インダクタンス
が増加するときには,それを増やさない向きに起電力がコイルに生じます.自己インダクタンス ![]() が大きいコイル程,自己誘導の現象は顕著になります.
が大きいコイル程,自己誘導の現象は顕著になります.
それでは,ここで,コイルの自己インダクタンスを表す式を求めておきましょう.コイルの単位長さ当たりの巻き数を
![]() 回
回![]() ,長さを
,長さを ![]() ,断面積を
,断面積を ![]() とします.このとき,コイル内部の磁場
とします.このとき,コイル内部の磁場 ![]() は,"定常電流の静磁場(ビオ-サバールの法則とアンペールの法則)" のChapterで見たように,
は,"定常電流の静磁場(ビオ-サバールの法則とアンペールの法則)" のChapterで見たように,
で与えられます.よって,磁束密度は,
![]() より,
より,
となります.ひと巻きのコイルを貫く磁束は ![]() なので,コイルの総巻き数は
なので,コイルの総巻き数は
![]() 回
回![]() より,コイル全体を貫く磁束は,
より,コイル全体を貫く磁束は,
です.ここで,
なので,
が自己インダクタンスを表す式になります.
自己誘導による誘導起電力 ![]() を表す式を求めてみましょう.ファラデーの電磁誘導の法則,
を表す式を求めてみましょう.ファラデーの電磁誘導の法則,
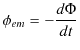
に,
を代入して,
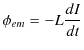
となります.電流の時間変化の割合が大きいほど,自己インダクタンスが大きいほど誘導起電力は大きくなります.
ここで,自己インダクタンス ![]() のコイル,
のコイル,![]() の抵抗,起電力
の抵抗,起電力 ![]() の電池とスイッチを直列につないだ回路を考えます.これをRL回路といいますが,図に示します.
の電池とスイッチを直列につないだ回路を考えます.これをRL回路といいますが,図に示します.
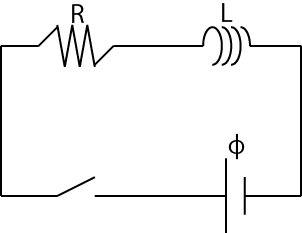
Figure11.5: 自己誘導1
スイッチを入れたとき,自己誘導が起こり,ゆっくりと電流が流れ始め,最終的には一定の電流が流れるようになります.このことを微分方程式で取り扱ってみましょう.時刻 ![]() に流れる電流を
に流れる電流を ![]() とすると,コイルには,
とすると,コイルには,
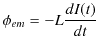
の誘導起電力が生じるので,抵抗には,
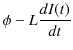
の電位差がかかることになります.ここで,オームの法則を抵抗に適用すると,
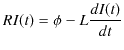
ですから,
となります.(11.6)式は定数係数の常微分方程式であり,一般論にしたがって,右辺を 0 とおいた同次方程式の解 ![]() に,(11.6)式を満たす特解
に,(11.6)式を満たす特解 ![]() を加えたものが一般解になります.まず,同次方程式を次のように解きます.
を加えたものが一般解になります.まず,同次方程式を次のように解きます.
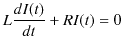 |
||
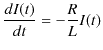 |
||
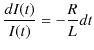 |
||
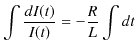 |
||
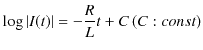 |
||
ここで,
![]() とおき,
とおき,![]() を
を ![]() とおき直すと,
とおき直すと,
となります.次に特解 ![]() ですが,これを定数であると仮定します.このとき,(11.6)式より,
ですが,これを定数であると仮定します.このとき,(11.6)式より,
と求められます.よって,一般解は,
となります.ここで,スイッチを入れた瞬間,電流が ![]() の場合を考えます.すなわち,初期条件を
の場合を考えます.すなわち,初期条件を ![]() で
で ![]() とします.このとき,
とします.このとき,
と定数 ![]() が決定します.故に,解は,
が決定します.故に,解は,
となります.この式は,スイッチを入れた後,時間の経過につれ,電流が ![]() から
から
![]() にだんだん近づいていく様子を表しています.
にだんだん近づいていく様子を表しています.![]() グラフを描くと図のようになります.
グラフを描くと図のようになります.
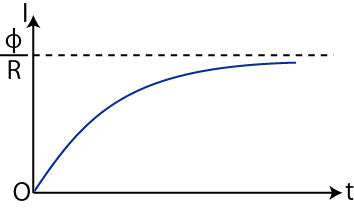
Figure11.6: 自己誘導2
一定の電流
![]() が流れていて,スイッチを切った場合も考えてみましょう.このとき,微分方程式は(11.6)式において電池の起電力
が流れていて,スイッチを切った場合も考えてみましょう.このとき,微分方程式は(11.6)式において電池の起電力 ![]() としたものになります.よって,微分方程式は同次方程式になり,その解は上の議論により,
としたものになります.よって,微分方程式は同次方程式になり,その解は上の議論により,
となります.一定の電流
![]() が流れている状態で,スイッチを切った瞬間
が流れている状態で,スイッチを切った瞬間 ![]() における電流の値は
における電流の値は
![]() なので,これを初期条件とすると,以下のように定数Aが決まります.
なので,これを初期条件とすると,以下のように定数Aが決まります.
故に,解は,
です.スイッチを切った後,電流は時間の経過とともに減少していることがわかります.
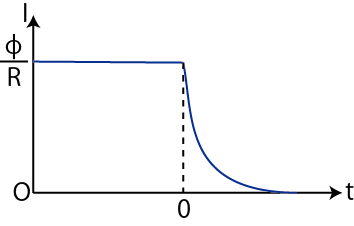
Figure11.7: 自己誘導3
11.3 静磁エネルギー
前のSectionの最後で見たように,RL回路において一定の電流が流れている状態でスイッチを切った後も,しばらくの間電流が流れて仕事をすることができます.これは,電流が流れているコイルにポテンシャルが溜まっているために起こる現象です.このポテンシャルを静磁エネルギーといいます.以下に,この静磁エネルギーを求めてみます.
RL回路において,抵抗が
![]() の場合を考えます.スイッチを入れて電流を流し始めるとき,自己誘導が起こりますが,その誘導起電力は,
の場合を考えます.スイッチを入れて電流を流し始めるとき,自己誘導が起こりますが,その誘導起電力は,
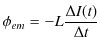
です.ここで,コイルは導線からできていますので抵抗が ![]() であることに注意すると,外からかかっている電位差は,
であることに注意すると,外からかかっている電位差は,
になります.この電位差のもとで,短い時間
![]() の間に
の間に
![]() の微小量の電荷が移動します.このとき,外からする微小な仕事
の微小量の電荷が移動します.このとき,外からする微小な仕事
![]() は,関係式
は,関係式
![]() を使って,(この場合,外から仕事をして電流を押し流しているので,正の仕事になります.)
を使って,(この場合,外から仕事をして電流を押し流しているので,正の仕事になります.)
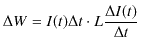
となります.スイッチを閉じた時刻 ![]() における電流
における電流 ![]() から始めて,ある時刻
から始めて,ある時刻 ![]() に電流
に電流 ![]() になったときを考えます.ある時刻
になったときを考えます.ある時刻 ![]() において,電流は定常状態になっていて一定の値をとるようになっていてもよいし,あるいはそれより以前の状態で電流が増加している状態でもよいです.この間になされた仕事を時刻
において,電流は定常状態になっていて一定の値をとるようになっていてもよいし,あるいはそれより以前の状態で電流が増加している状態でもよいです.この間になされた仕事を時刻 ![]() から
から ![]() まで積分して求めます.(ここで,短い時間
まで積分して求めます.(ここで,短い時間
![]() を限りなく
を限りなく ![]() に近づける極限をとります.)
に近づける極限をとります.)
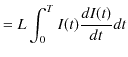 |
||
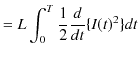 |
||
![$\displaystyle =\dfrac{L}{2}[I(t)^{2}]_{0}^{T}$](ja_Chapter11_ElectromagneticInduction_FaradaysLaw_images/img142.png) |
||
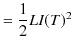 |
||
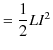 |
この外からなされた仕事をされた分だけ,静磁エネルギーとして蓄えられたことになります.故に,静磁エネルギー ![]() は,
は,
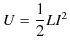
で与えられます.ここで,![]() は一定の状態になっている場合もあれば,増加している状態のときもあり,どちらにしても,その瞬間の電流の値です.(電流の変化があまり速くない場合を考えて,その瞬間においては静磁場が生じているとします.)
は一定の状態になっている場合もあれば,増加している状態のときもあり,どちらにしても,その瞬間の電流の値です.(電流の変化があまり速くない場合を考えて,その瞬間においては静磁場が生じているとします.)
以上の議論はコイルに蓄えられた静磁エネルギーがポテンシャルであるという遠隔作用の立場から説明しました.コイルの静磁エネルギーは,コンデンサーに蓄えられた静電エネルギーと対比されるものですが,そのときと同じように,近接作用の立場から捉えなおしてみます.つまり,静磁エネルギーは空間の歪みである磁場に蓄えられていると考えるのです.前のSectionで求めたように,コイルの自己インダクタンスは,
でした.したがって,静磁エネルギーは,
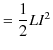 |
||
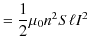 |
||
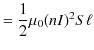 |
||
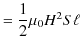 |
となります.ここで,
![]() はコイルの体積なので,単位体積当たりの静磁エネルギー
はコイルの体積なので,単位体積当たりの静磁エネルギー
![]() は,
は,
となります.さらに変形して,
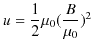
ですから,
です.(11.7)式と,(11.8)式が近接作用による静磁エネルギーを表した式です.