Chapter3 ニュートンの法則

3.1 ニュートンの三法則

物体の運動と物体にはたらく力について，次のニュートンの三法則が成立します．

法則3.1(第一法則（慣性の法則）) "物体に力がはたらかないか，つりあっているとき，物体は静止したままでいるか，または等速直線運動を続けます．"

法則3.2(第二法則（運動の法則）) "物体に力がはたらくとき，力の向きに加速度が生じます．加速度の大きさは力の大きさに比例し，質量に反比例します．"

法則3.3(第三法則（作用・反作用の法則）) "物体 $ A$ が物体 $ B$ に力（作用）を及ぼすとき，必然的に物体 $ B$ は物体 $ A$ に力（反作用）を及ぼしかえします．この2力は大きさが同じで，向きが反対で，同一作用線上にあります．"

第二法則は次式のように表すことができます．

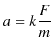
$\displaystyle a=k\dfrac{F}{m}$

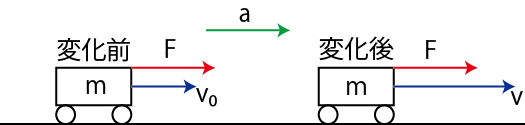
ただし， $ a[m/s^{2}]$ は加速度の大きさ，$ F[kgw]$ は力の大きさ，$ m[kg]$ は質量，$ k$ は比例定数です．第二法則（運動の法則）は力が変化する場合もその瞬間，その瞬間においても成立しますが，一定の力 $ F[kgw]$ がはたらくシンプルな場合について，図を示しておきます．（$ v[m/s]$ は速度です．）

運動の法則

Figure3.1: 運動の法則

ここで，比例定数を簡単な数1にするために，力の単位 $ [N]$（ニュートン）を次のように定義します．

定義3.1(力2) "$ 1[N]$ =質量 $ 1[kg]$ の物体に $ 1[m/s^{2}]$ の加速度を生じさせる力の大きさ"

このとき，上式は $ ma=F$ という式になりますが，この式を運動方程式と言います．運動方程式を向きまで含めて表すためにベクトルを使って，4通りに示しておきます．

$\displaystyle \fbox{$m\vec{a}=\vec{F}$}$ (3.1)
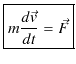$\displaystyle \fbox{$m\dfrac{d\vec{v}}{dt}=\vec{F}$}$ (3.2)
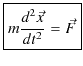$\displaystyle \fbox{$m\dfrac{d^{2}\vec{x}}{dt^{2}}=\vec{F}$}$ (3.3)
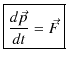$\displaystyle \fbox{$\dfrac{d\vec{p}}{dt}=\vec{F}$}$ (3.4)

最後の式の $ \vec{p}\equiv m\vec{v}$ は運動量です．これらの方程式は運動と力の関係を表していますが，上で単位 $ [N]$ を定めたように，力の定義式にもなっています．（力の2番目の定義です．1番目の定義は，後の "質量" のSectionを見て下さい．）また，右辺で $ \vec{F}=0[N]$ とすると，左辺で加速度が $ 0[m/s^{2}]$ になり，慣性の法則とも矛盾しません．運動方程式は力学の理論において根幹をなす方程式です．

 

3.2 万有引力の法則

2つの物体について，その間には万有引力と呼ばれる引力がはたらきます．その大きさ $ F[N]$ は次式で表されます．

法則3.4(万有引力の法則)

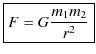$\displaystyle \fbox{$F=G\dfrac{m_{1}m_{2}}{r^{2}}$}$ (3.5)

ここで，$ m_{1}[kg]$ と $ m_{2}[kg]$ はそれぞれの物体の質量，$ r[m]$ は2物体間の距離です．

万有引力

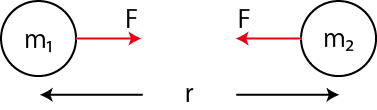
Figure3.2: 万有引力

また， $ G[N\cdot m^{2}\cdot kg^{-2}]$ は万有引力定数で，1798年にキャベンディッシュにより測定され，次の値であることがわかっています．

$\displaystyle G=6.67\times10^{-11}[N\cdot m^{2}\cdot kg^{-2}]$

万有引力は全ての物体の間ではたらく力です．重力の正体は万有引力ですが，素粒子論では万有引力のことを重力と呼ぶことが一般的です．また，何故重力（万有引力）がはたらくのかという根本的理由についても言及しておきます．ニュートンが万有引力の法則を発見したときは，その理由についてはブラックボックスだったと考えられます．20世紀になり，アインシュタインが重力（万有引力）の理論である一般相対性理論を完成した際は，重力（万有引力）は時空の曲がりによって説明されました．その後の量子重力理論，更には弦理論においては，まさに重力（万有引力）の本質を解明しようとする試みがなされているのです．

 

3.3 質量

重さと質量は，本質的に異なる物理量です．重さとは物体にはたらく重力の大きさであり，場所によってその値が違ってきます．力の1番目の定義として，

定義3.2(力1) "$ 1[kgw]$=地球上において，質量 $ 1[kg]$ の物体にはたらく重力の大きさ"

と $ [kgw]$ という単位を定めることができます．実は，地球上でも重力の測定値は僅かずつではありますが異なります．また，地球上で $ 60[kgw]$の重さの物体を月面上で測定すると，約6分の1の約 $ 10[kgw]$ になることはよく知られています．（場所によって重力の値が異なる理由は，重力の本質が万有引力であり，天体の質量や天体の中心までの距離により重力の大きさが決まるためです．）一方，質量は物質の量であり，場所が違ってもその値は変わりません．地球上で $ 60[kg]$ の質量の物体は，月面上でも $ 60[kg]$ であり，宇宙の全ての場所で $ 60[kg]$ です．（質量の単位には $ [kg]$ を使います．）重さよりも，質量の方が本質的な物理量であるということが言えます．究極的には，質量とは素粒子の属性であり，電磁気学における電荷と同じような性質をもつ物理量です．（ただし，質量が正の値のみをとる量なのに対し，電荷は正と負のどちらかをとることができる量です．）

　質量は物質の量ですが，上記の運動方程式と万有引力の法則の物理法則の中に含まれています．ここで，運動方程式に含まれる質量を慣性質量といい，万有引力の法則に含まれる質量を重力質量といいます．この2つの質量は本来，別物であり，同じであるという根拠は何もありません．しかし，何度実験によって測定しても，その差異はほとんど見出すことはできません．そこで，この2つの質量の同一性を自然の本質であると考え，原理にまで止揚したのが，アインシュタインの一般相対性理論における等価原理です．

 

3.4 力学の体系

上に述べた4つの法則は力学の基礎を成すものです．4つの法則は実験によって直接確かめられます．さらに，4つの法則から理論的に演繹された結論も実験によって検証されます．例えば，後のChapterで取り扱う力学的エネルギー保存則，運動量保存則，角運動量保存則はニュートンの3法則の枠内で導出され，それぞれ実験で確認されます．他にも，単振り子の周期の式から惑星の運動に至るまで，多くの現象についての結論が，ニュートンの三法則と万有引力の法則から演繹され，実験で実証されています．力学の体系は閉じているのです．体系が閉じているが故に力学は正しいのです．（19世紀までは正しかったと言った方が正確ですが．）

　ここに，物理学の典型的パターンが見受けられます．幾つかの実験事実から帰納された法則が一旦形成されると，その法則から多くの事象が演繹されます．その事象は実験で検証され，ひとつでも確実な反例が見つかると法則は破綻します．19世紀までの力学は確固たるものでしたが，20世紀になって反例が発見され破綻しました．その結果，誕生したのが相対性理論と量子力学です．相対性理論においては絶対空間と絶対時間といったニュートン力学の根底が否定され，相対的な時空という概念が確立されました．量子力学においても幾つかの革命的な考え方が導入されました．まず，エネルギーという物理量が不連続で跳び跳びの値をとることが認識されました．また，ニュートン力学では運動方程式という微分方程式が立てられ，初期条件を与えれば運動は決定論的に決まってしまいますが，量子力学においては，量子論的概念である量子状態とそれが従うシュレディンガー方程式（これも微分方程式です．）によって確率的に系が記述されます．その後，力学は古典力学として位置付けられ，その法則は限られた範囲内でのみ成立することになりました．つまり，相対論的効果が効いてこないためには，運動の速さが光速に比べて非常に遅いこと，量子論的効果が効いてこないためには，マクロな現象を取り扱うこと，これらのことが，古典力学が有効であるための条件です．ただし，力学的エネルギー保存則，運動量保存則，角運動量保存則の3つの保存則は現代物理の枠の中でも成立することがわかっています．

 

3.5 MKS単位系

物理量の中で，長さ，質量，時間は最も基本的なものです．ここで，長さの単位に $ [m]$，質量の単位に $ [kg]$，時間の単位に $ [s]$ を採用する単位系をMKS単位系と言います．長さ，質量，時間以外の物理量，例えば，速度，加速度，力といったもの，あるいは今後出てくる運動量，エネルギー等の単位は全て長さ，質量，時間の単位の組み合わせでつくることができます．ただし，電磁気学まで考えた場合は，さらに電流の単位 $ [A]$ を基本的な単位として取り入れる必要があります．（これをMKSA単位系と言います．）Group古典物理学の中では，MKS単位系またはMKSA単位系で統一して取り扱うことにします．