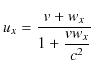Chapter3 特殊相対性理論の世界
3.1 同時性の問題
特殊相対性理論を認めると,常識では考えられないような結論が幾つか導かれます.初等的な取扱い,そしてLorentz変換,Lorentz逆変換とMinkowski時空図を用いて,以下議論していきましょう.
最初に,同時性の問題を見ておきます.この問題は,"特殊相対性原理と光速不変の原理" のChapterの最後に,光速不変の原理を用いて取り扱いました.そのときの状況を表す2つの図を再掲しておきます.
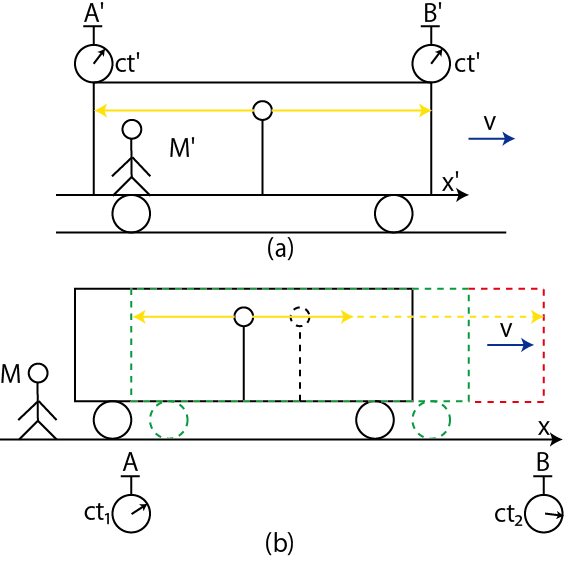
Figure3.1: 同時性3
等速直線運動している列車の中央から光のフラッシュを放った場合,列車に乗り込んだ観測者(慣性系
![]() )には,列車の両端に同時に光が到着するのに対して,地面から見てる観測者(慣性系
)には,列車の両端に同時に光が到着するのに対して,地面から見てる観測者(慣性系 ![]() )に対しては同時ではありません.光速不変の原理より,列車に対しても,地面に対しても,光の速さが同じ
)に対しては同時ではありません.光速不変の原理より,列車に対しても,地面に対しても,光の速さが同じ ![]() になることが話の肝心な点でした.この同時性の問題を,Lorentz逆変換を用いて取り扱っておきます.時間1次元と空間1次元(
になることが話の肝心な点でした.この同時性の問題を,Lorentz逆変換を用いて取り扱っておきます.時間1次元と空間1次元(![]() 成分)からなる2次元時空を考えます.(このChapterでは,以下,主に2次元時空を考えます.)慣性系
成分)からなる2次元時空を考えます.(このChapterでは,以下,主に2次元時空を考えます.)慣性系 ![]() に対して,
に対して,![]() 方向に速さ
方向に速さ ![]() で等速直線運動している慣性系
で等速直線運動している慣性系
![]() という状況です.慣性系
という状況です.慣性系
![]() において同時に起こった2つの事象
において同時に起こった2つの事象
![]() と
と
![]() は,
は,![]() においてはそれぞれ
においてはそれぞれ
![]() と
と
![]() とおくことができます.
とおくことができます.![]() における時間の成分を同じ文字で表さなかったのは,事象が同時に起こったか否か,保証されていないためです.Lorentz逆変換の時間成分の式,
における時間の成分を同じ文字で表さなかったのは,事象が同時に起こったか否か,保証されていないためです.Lorentz逆変換の時間成分の式,
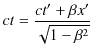
より,次の量を計算します.
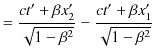 |
||
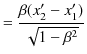 |
ここで,
![]() なので,
なので,
![]() となり,やはり,
となり,やはり,![]() において同時性が破れていることが確認されます.2次元時空図も見ておきましょう.
において同時性が破れていることが確認されます.2次元時空図も見ておきましょう.
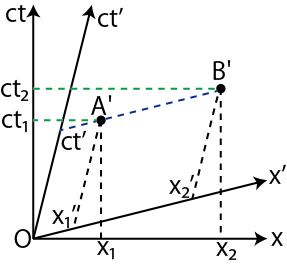
Figure3.2: 同時性4
世界点
![]() と世界点
と世界点
![]() は,慣性系
は,慣性系
![]() に対しては,同時刻
に対しては,同時刻 ![]() です.(青色の破線を見て下さい.)一方,慣性系
です.(青色の破線を見て下さい.)一方,慣性系 ![]() に対しては,
に対しては,
![]() の時刻が
の時刻が ![]() で,
で,
![]() の時刻が
の時刻が ![]() となり,同時ではありません.(2本の緑色の破線を見て下さい.
となり,同時ではありません.(2本の緑色の破線を見て下さい.
![]() で,
で,
![]() の方が先に起こります.)
の方が先に起こります.)
議論のついでに,慣性系 ![]() において,同時に起こった2つの事象
において,同時に起こった2つの事象
![]() と
と
![]() に対して,慣性系
に対して,慣性系
![]() では同時性が破れていることも確認しておきましょう.この場合,慣性系
では同時性が破れていることも確認しておきましょう.この場合,慣性系
![]() に対して,
に対して,![]() の負の方向に速さ
の負の方向に速さ ![]() で等速直線運動している慣性系
で等速直線運動している慣性系 ![]() という状況を設定しておきます.
という状況を設定しておきます.
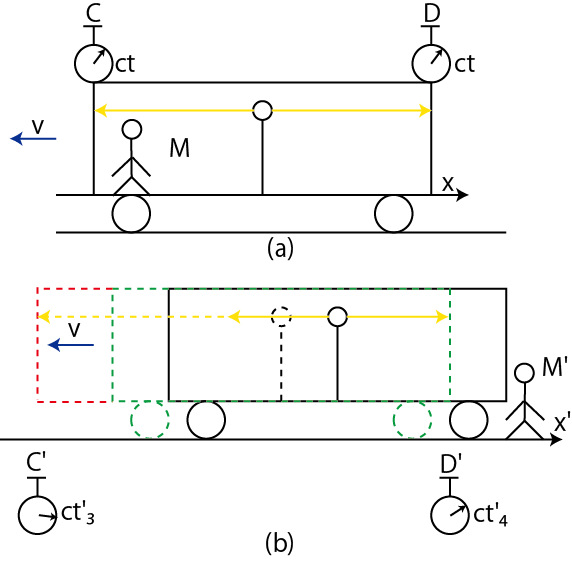
Figure3.3: 同時性5
2つの事象は
![]() においては,それぞれ
においては,それぞれ
![]() と
と
![]() とおくことができます.
とおくことができます.
![]() における時間の成分を同じ文字で表さなかったのは,事象が同時に起こったか否か,保証されていないためです.Lorentz変換の時間成分の式,
における時間の成分を同じ文字で表さなかったのは,事象が同時に起こったか否か,保証されていないためです.Lorentz変換の時間成分の式,
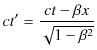
により,次の量を計算します.
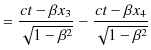 |
||
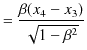 |
このとき,
![]() なので,
なので,
![]() となります.同時性が破れていることが確認できました.2次元時空図でも同時性が破れていることが確かめられます.("同時性6" の図を見て下さい.)
となります.同時性が破れていることが確認できました.2次元時空図でも同時性が破れていることが確かめられます.("同時性6" の図を見て下さい.)
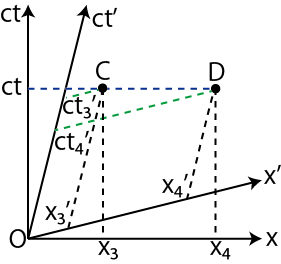
Figure3.4: 同時性6
世界点
![]() と世界点
と世界点
![]() は,慣性系
は,慣性系 ![]() に対しては,同時刻
に対しては,同時刻 ![]() です.(青色の破線を見て下さい.)一方,慣性系
です.(青色の破線を見て下さい.)一方,慣性系
![]() に対しては,
に対しては,
![]() の時刻が
の時刻が ![]() で,
で,
![]() の時刻が
の時刻が ![]() となり,同時ではありません.(2本の緑色の破線を見て下さい.
となり,同時ではありません.(2本の緑色の破線を見て下さい.
![]() で,
で,
![]() の方が先に起こります.)
の方が先に起こります.)
3.2 時間の遅れ
引き続き時間についてですが,Newton力学の世界とは全く違う特殊相対論的な現象として,
"動いている慣性系の時間は遅れます."
ということについて考えましょう.まず,直観的に理解しやすい例として,光時計と呼ばれるものを取り扱います.これは光の進んだ距離によって時間を計る装置です."時間の遅れ1" の図を見て下さい.
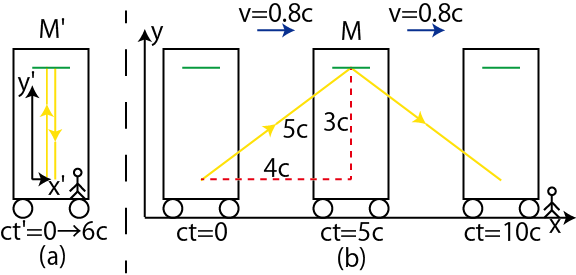
Figure3.5: 時間の遅れ1
地球の大きさよりも巨大で,光速の ![]() パーセントの速さで等速直線運動している乗り物を考えます.(思考実験ですから設定可能です.)乗り物に乗り込んだ観測者(慣性系
パーセントの速さで等速直線運動している乗り物を考えます.(思考実験ですから設定可能です.)乗り物に乗り込んだ観測者(慣性系
![]() )から見て,進行方向と垂直に光が往復しています.(図の緑色の線は鏡です.)慣性系
)から見て,進行方向と垂直に光が往復しています.(図の緑色の線は鏡です.)慣性系
![]() に対して,光速は
に対して,光速は ![]() です.時間が,片道
です.時間が,片道 ![]() ,往復
,往復 ![]() 経過したとします.(図の (a) を見て下さい.)このとき,乗り物の外から見た観測者(慣性系
経過したとします.(図の (a) を見て下さい.)このとき,乗り物の外から見た観測者(慣性系 ![]() )に対しては,光が一往復するのに何秒かかるでしょうか?
)に対しては,光が一往復するのに何秒かかるでしょうか? ![]() に対する光速は,光速不変の原理より,やはり
に対する光速は,光速不変の原理より,やはり ![]() です.しかし,乗り物が運動していますので,図の (b) のように,光は進行方向に対して斜めに進みます.そして,図の直角3角形は3平方の定理より,
です.しかし,乗り物が運動していますので,図の (b) のように,光は進行方向に対して斜めに進みます.そして,図の直角3角形は3平方の定理より,![]() の辺の比を持ちます.これから,
の辺の比を持ちます.これから,![]() においては,光が一往復するのに
においては,光が一往復するのに ![]() かかることがわかります.動いている慣性系
かかることがわかります.動いている慣性系
![]() においては,時間がゆっくりと進み,遅れることが理解されますね.議論を一般化して,乗り物の速さを
においては,時間がゆっくりと進み,遅れることが理解されますね.議論を一般化して,乗り物の速さを ![]() ,
,
![]() において光が一往復するのに要する時間を
において光が一往復するのに要する時間を ![]() ,
,![]() において光が一往復するのに要する時間を
において光が一往復するのに要する時間を ![]() とします.("時間の遅れ2" の図を見て下さい.)
とします.("時間の遅れ2" の図を見て下さい.)
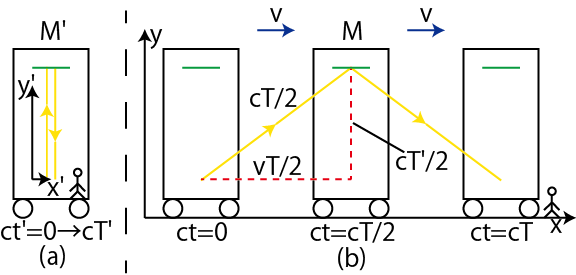
Figure3.6: 時間の遅れ2
ここで,直角3角形に対して,3平方の定理を使い計算します.
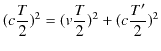 |
||
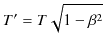 |
やはり,動いている慣性系
![]() における光一往復の時間
における光一往復の時間 ![]() の方が,慣性系
の方が,慣性系 ![]() における光一往復の時間
における光一往復の時間 ![]() よりも小さく,遅れることがわかります.もっとも,慣性系間の速さ
よりも小さく,遅れることがわかります.もっとも,慣性系間の速さ ![]() が光速
が光速 ![]() に比べて小さく,
に比べて小さく,
![]() が無視できる場合は,時間の遅れは微々たるものです.
が無視できる場合は,時間の遅れは微々たるものです.
時間の遅れをLorentz逆変換を用いて取り扱いましょう.ここでも,慣性系 ![]() に対して,慣性系
に対して,慣性系
![]() が速さ
が速さ ![]() で等速直線運動している場合を考えます.
で等速直線運動している場合を考えます.
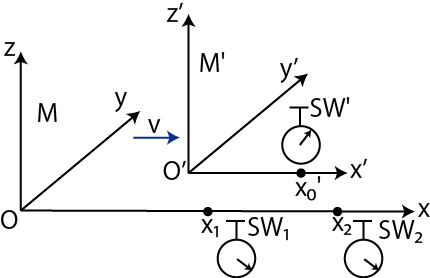
Figure3.7: 時間の遅れ3
![]() の
の ![]() にストップウォッチ
にストップウォッチ ![]() があり,
があり,![]() に
に ![]() があり,それぞれ
があり,それぞれ ![]() に対して固定されています.(
に対して固定されています.(![]() と
と ![]() は,
は,![]() において同時刻を示すように設定されているものとします.その方法は,
において同時刻を示すように設定されているものとします.その方法は,![]() と
と ![]() の中点
の中点
![]() から光のフラッシュを放ち,到着する時刻を同時刻とすればよいです.)また,
から光のフラッシュを放ち,到着する時刻を同時刻とすればよいです.)また,
![]() の
の ![]() にストップウォッチ
にストップウォッチ ![]() が置かれています.
が置かれています.![]() が時刻
が時刻 ![]() を示したとき,
を示したとき,![]() が
が ![]() を通過したとします.このとき,
を通過したとします.このとき,![]() の座標は
の座標は
![]() から見て,
から見て,
![]() です.この事象を
です.この事象を ![]() から見ると,
から見ると,
![]() となります.その後,
となります.その後,![]() が時刻
が時刻 ![]() を示したとき,
を示したとき,![]() が
が ![]() を通過したとします.このとき,
を通過したとします.このとき,![]() の座標は
の座標は
![]() から見て,
から見て,
![]() です.この事象を
です.この事象を ![]() から見ると,
から見ると,
![]() となります.ここで,Lorentz逆変換の時間成分の式,
となります.ここで,Lorentz逆変換の時間成分の式,
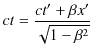
より,
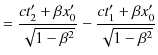 |
||
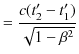 |
ですから,
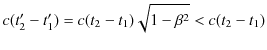
となります.ここで,
とおくと,
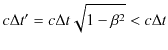 |
||
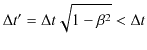 |
です.つまり,![]() において,時間
において,時間 ![]() 経過したとき,動いている
経過したとき,動いている
![]() では時間
では時間
![]() しか経過していないことになります.これが,運動している時計は遅れるという現象です.例えば,
しか経過していないことになります.これが,運動している時計は遅れるという現象です.例えば,![]() のときは,
のときは,
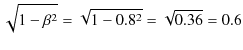
となりますから,
![]() となります.
となります.
![]() のときは,
のときは,
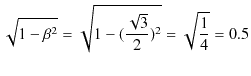
となりますから,
![]() となります.もっとも
となります.もっとも
![]() は,運動の速さ
は,運動の速さ ![]() が光速に比べて小さいときは,およそ
が光速に比べて小さいときは,およそ ![]() になって,ほとんど影響を及ぼしません.(光速で運動する物体では,
になって,ほとんど影響を及ぼしません.(光速で運動する物体では,
![]() となって,
となって,
![]() となります.光速で運動する物体では時間が経過しないという結果になります.)自分が静止している座標系で測定する時間を,その物体の固有時間といいます.ここでは,
となります.光速で運動する物体では時間が経過しないという結果になります.)自分が静止している座標系で測定する時間を,その物体の固有時間といいます.ここでは,![]() が固有時間になります.固有時間であることを強調するときは,
が固有時間になります.固有時間であることを強調するときは,![]() を
を
![]() と表すこともあります.2次元時空図で状況を表すと,"時間の遅れ4" の図のようになります.
と表すこともあります.2次元時空図で状況を表すと,"時間の遅れ4" の図のようになります.
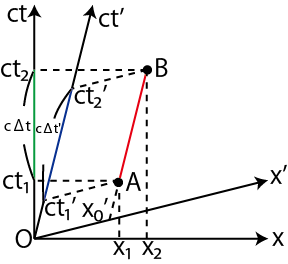
Figure3.8: 時間の遅れ4
![]() での経過時間
での経過時間
![]() は緑色の線の長さで,動いている
は緑色の線の長さで,動いている
![]() での経過時間
での経過時間
![]() は青色の線の長さです.図の上では青色の線が緑色の線よりも長くなっていますが,その値の大小関係は計算で示したように逆になります.(
は青色の線の長さです.図の上では青色の線が緑色の線よりも長くなっていますが,その値の大小関係は計算で示したように逆になります.(
![]() でしたね.)
でしたね.)
特殊相対性原理より,![]() と
と
![]() は完全に同等のはずです.
は完全に同等のはずです.![]() に対して,
に対して,
![]() が等速直線運動しているということは,
が等速直線運動しているということは,
![]() を基準にして,
を基準にして,![]() が逆方向に等速直線運動していると考えることもできますね.この場合,時間が遅れるのは
が逆方向に等速直線運動していると考えることもできますね.この場合,時間が遅れるのは ![]() の方になってしまいます.これは,明らかに時間が遅れるのは
の方になってしまいます.これは,明らかに時間が遅れるのは
![]() の方であるという,上記の主張と矛盾しているように思えます.この矛盾を時間のparadoxといいます.しかし,両方とも正しいのです.立場によって,主張は異なるのは,慣性系が完全に同等であることを意味します.
の方であるという,上記の主張と矛盾しているように思えます.この矛盾を時間のparadoxといいます.しかし,両方とも正しいのです.立場によって,主張は異なるのは,慣性系が完全に同等であることを意味します.![]() に対して
に対して
![]() が等速直線運動していると考えるときは,遅れる時計
が等速直線運動していると考えるときは,遅れる時計 ![]() は,
は,
![]() に対して静止していて,
に対して静止していて,![]() に対しては運動しています.逆に,
に対しては運動しています.逆に,
![]() に対して
に対して ![]() が等速直線運動していると考えるときは,遅れる時計
が等速直線運動していると考えるときは,遅れる時計 ![]() は,
は,![]() に対して静止していて,
に対して静止していて,
![]() に対しては運動しています.つまり,2つの立場での事象は異なっているのです.このことに注意しながら,Lorentz変換による計算とMinkowski時空図を確認しましょう.
に対しては運動しています.つまり,2つの立場での事象は異なっているのです.このことに注意しながら,Lorentz変換による計算とMinkowski時空図を確認しましょう.
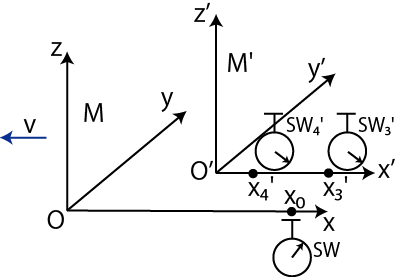
Figure3.9: 時間の遅れ5
![]() の
の ![]() にストップウォッチ
にストップウォッチ ![]() があり,
があり,![]() に
に ![]() があり,それぞれ
があり,それぞれ
![]() に対して固定されています.(
に対して固定されています.(![]() と
と ![]() は,
は,
![]() において同時刻を示すように設定されているものとします.前述のフラッシュを使う方法を
において同時刻を示すように設定されているものとします.前述のフラッシュを使う方法を
![]() において行います.)また,
において行います.)また,![]() にストップウォッチ
にストップウォッチ ![]() が
が![]() に対して固定されています.
に対して固定されています.![]() が時刻
が時刻 ![]() を示したとき,
を示したとき,![]() が
が ![]() を通過したとします.このとき,
を通過したとします.このとき,![]() の座標は
の座標は ![]() からみて,
からみて,
![]() です.この事象を
です.この事象を
![]() から見ると,
から見ると,
![]() となります.その後,
となります.その後,![]() が時刻
が時刻 ![]() を示したとき,
を示したとき,![]() が
が ![]() を通過したとします.このとき,
を通過したとします.このとき,![]() の座標は
の座標は ![]() から見て,
から見て,
![]() です.この事象を
です.この事象を
![]() から見ると,
から見ると,
![]() となります.
となります.
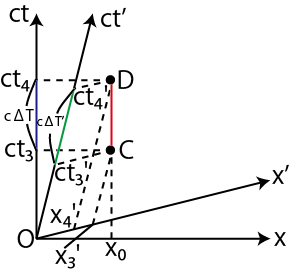
Figure3.10: 時間の遅れ6
ここで,Lorentz変換の時間成分の式,
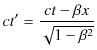
より,
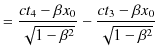 |
||
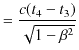 |
ですから,
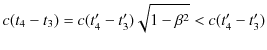
となります.ここで,
とおくと,
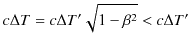 |
||
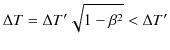 |
です.(この場合,慣性系 ![]() に固定された時計の時間を問題としていますので,固有時間は
に固定された時計の時間を問題としていますので,固有時間は ![]() になります.)事象
になります.)事象 ![]() と
と ![]() は違いますので,主張の相違があっても問題はありません.Section 前半の議論で出てきた不等式と比較するため,
は違いますので,主張の相違があっても問題はありません.Section 前半の議論で出てきた不等式と比較するため,
![]() としてみましょう.このとき,
としてみましょう.このとき,
が成立し,矛盾していません.
3.3 双子のparadox
時間のparadoxは解消できましたが,時間について,さらに次のようなparadoxを考えることができます.これは,2つの時計を直接比較できる例です.双子の ![]() と
と ![]() という兄弟が地球にいるとします.
という兄弟が地球にいるとします.![]() は宇宙旅行に出かけ,
は宇宙旅行に出かけ,![]() は地球に留まるとしましょう.
は地球に留まるとしましょう.![]() は地球から等速直線運動した後,ある時刻で瞬時に反転し,行きと同じ速さで等速直線運度して地球に帰ってきました.(議論を簡単にするため,反転は瞬時に行われるとしました.このためには無限大の力が必要ですが,思考実験においては可能です.)2次元で考えましょう.地球に固定した座標系を
は地球から等速直線運動した後,ある時刻で瞬時に反転し,行きと同じ速さで等速直線運度して地球に帰ってきました.(議論を簡単にするため,反転は瞬時に行われるとしました.このためには無限大の力が必要ですが,思考実験においては可能です.)2次元で考えましょう.地球に固定した座標系を ![]() ,
,![]() の行きのロケットに固定した座標系を
の行きのロケットに固定した座標系を
![]() ,
,![]() の帰りのロケットに固定した座標系を
の帰りのロケットに固定した座標系を
![]() とします.
とします.
![]() は全て慣性系であり,
は全て慣性系であり,![]() が帰還したとき,
が帰還したとき,![]() の立場から考えると,運動しているのは
の立場から考えると,運動しているのは ![]() で,
で,![]() は自分より若くなっていると主張し,
は自分より若くなっていると主張し,![]() の立場から考えると,運動しているのは
の立場から考えると,運動しているのは ![]() で,
で,![]() は自分より若くなっていると主張するでしょう.この矛盾を双子のparadoxといいます.結論から言うと,正しいのは地球に留まった
は自分より若くなっていると主張するでしょう.この矛盾を双子のparadoxといいます.結論から言うと,正しいのは地球に留まった ![]() の主張,つまり,
の主張,つまり,![]() の方が若いという主張です.
の方が若いという主張です.
Paradoxを解くためには,この状況の2次元時空図を描くと理解できます.
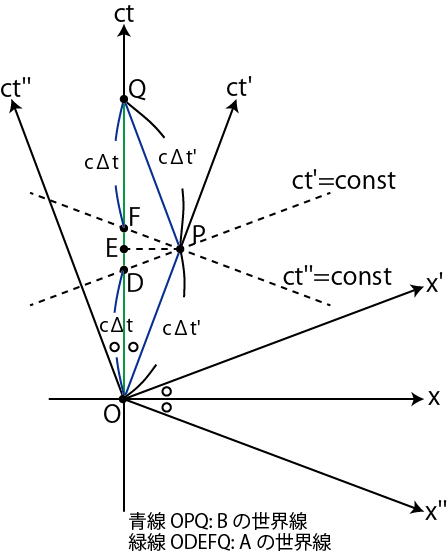
Figure3.11: 双子のparadox
青線 ![]() が
が ![]() の世界線,緑線
の世界線,緑線 ![]() が
が ![]() の世界線です.前Sectionの結論より,
の世界線です.前Sectionの結論より,![]() の世界線
の世界線 ![]() (経過時間
(経過時間 ![]() )に対して,
)に対して,![]() の世界線
の世界線 ![]() (経過時間
(経過時間 ![]() )においては,
)においては,
![]() が成立し,
が成立し,![]() の方がゆっくりと時間が経過します.
の方がゆっくりと時間が経過します.![]() の世界線
の世界線 ![]() (経過時間
(経過時間 ![]() )に対して,
)に対して,![]() の世界線
の世界線 ![]() (経過時間
(経過時間 ![]() )においても,
)においても,
![]() が成立し,
が成立し,![]() の方がゆっくりと時間が経過します.さらに,
の方がゆっくりと時間が経過します.さらに,![]() が,世界点
が,世界点 ![]() において,一瞬で反転する際,
において,一瞬で反転する際,![]() の方は世界線
の方は世界線 ![]() の分だけ時間が経過しています.以上のことから,
の分だけ時間が経過しています.以上のことから,![]() の方が,
の方が,![]() よりも時間が遅れ,年を取らないという結論になり,paradoxは解消します.
よりも時間が遅れ,年を取らないという結論になり,paradoxは解消します.
3.4 空間の収縮(Lorentz収縮)
特殊相対性理論では,空間についての現象でもNewton力学と相いれない結論が導かれます.それは,
"動いている慣性系の空間は収縮します."
という現象です.ここでも,慣性系 ![]() に対して,慣性系
に対して,慣性系
![]() が
が ![]() 方向に速さ
方向に速さ ![]() で等速直線運動をしている状況を考えます.
で等速直線運動をしている状況を考えます.
![]() の
の ![]() 軸に沿って置かれている長さ
軸に沿って置かれている長さ ![]() の棒を,
の棒を,![]() において同時刻に観測する場合を考察します.(同時刻の設定方法は,前述のフラッシュを使う方法です.)
において同時刻に観測する場合を考察します.(同時刻の設定方法は,前述のフラッシュを使う方法です.)
![]() における棒の両端の
における棒の両端の ![]() 座標を
座標を
![]() とし,棒の両端の
とし,棒の両端の ![]() 座標を,
座標を,![]() における同時刻
における同時刻 ![]() のとき,
のとき,
![]() とします.
とします.![]() における,この2つの事象を
における,この2つの事象を
![]() とします.これらを
とします.これらを
![]() から見ると,
から見ると,
![]() となります.
となります.
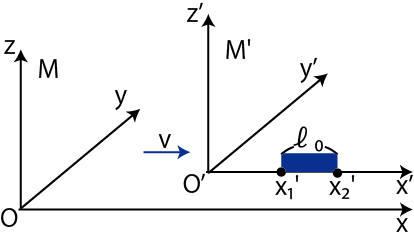
Figure3.12: 空間の収縮1
Lorentz変換により議論を進めましょう.ここで,Lorentz変換の ![]() 成分の式,
成分の式,
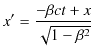
より,
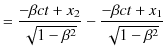 |
||
となります.ここで,
![]() は
は ![]() での棒の長さを表しますので,これを
での棒の長さを表しますので,これを ![]() とおきます.このとき,
とおきます.このとき,
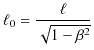 |
||
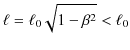 |
となります.つまり,慣性系 ![]() から観測した棒の長さ
から観測した棒の長さ ![]() は,
は,
![]() での長さ
での長さ ![]() より短いという結論になります.これが,動いている棒の長さが縮むという現象です.例えば,
より短いという結論になります.これが,動いている棒の長さが縮むという現象です.例えば,![]() のときは,
のときは,
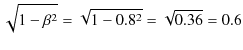
となりますから,
![]() となります.
となります.
![]() のときは,
のときは,
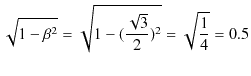
となりますから,
![]() となります.棒だけではなく,その入れ物である空間そのものが縮んでいると考えられます.すなわち,動いている空間は収縮すると言えます.(自分が静止している座標系で測定する空間の長さを固有空間といいましょう.この場合,
となります.棒だけではなく,その入れ物である空間そのものが縮んでいると考えられます.すなわち,動いている空間は収縮すると言えます.(自分が静止している座標系で測定する空間の長さを固有空間といいましょう.この場合,![]() は
は
![]() に対して固有空間です.)状況を2次元時空図 "空間の収縮2" で表しておきます.
に対して固有空間です.)状況を2次元時空図 "空間の収縮2" で表しておきます.
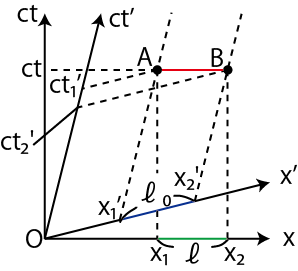
Figure3.13: 空間の収縮2
時間の遅れの場合と同様に,特殊相対性原理より,![]() と
と
![]() は完全に同等のはずです.
は完全に同等のはずです.![]() に対して,
に対して,
![]() が等速直線運動しているということは,
が等速直線運動しているということは,
![]() を基準にして,
を基準にして,![]() が等速直線運動していると考えることもできます.この場合,長さが縮むのは,
が等速直線運動していると考えることもできます.この場合,長さが縮むのは,![]() におかれた棒ということになります.これは,明らかに長さが縮むのは
におかれた棒ということになります.これは,明らかに長さが縮むのは
![]() におかれた棒であるという,上記の主張と矛盾しているように思えます.この矛盾を空間のparadoxといいます.しかし,両方とも正しいのです.立場によって主張が異なるのは,慣性系が完全に同等であることを意味します.
におかれた棒であるという,上記の主張と矛盾しているように思えます.この矛盾を空間のparadoxといいます.しかし,両方とも正しいのです.立場によって主張が異なるのは,慣性系が完全に同等であることを意味します.![]() に対して
に対して
![]() が等速直線運動していると考えるときは,棒は
が等速直線運動していると考えるときは,棒は
![]() に対して静止していて,
に対して静止していて,![]() に対しては運動しています.逆に,
に対しては運動しています.逆に,
![]() に対して
に対して ![]() が等速直線運動していると考えるときは,棒は
が等速直線運動していると考えるときは,棒は![]() に対して静止していて,
に対して静止していて,
![]() に対しては運動しています.つまり,2つの立場での事象は異なっているのです.このことに注意しながら,Lorentz逆変換による計算とMinkowski時空図を確認しましょう.慣性系
に対しては運動しています.つまり,2つの立場での事象は異なっているのです.このことに注意しながら,Lorentz逆変換による計算とMinkowski時空図を確認しましょう.慣性系
![]() に対して,慣性系
に対して,慣性系 ![]() が
が![]() の負の方向に速さ
の負の方向に速さ ![]() で等速直線運動をしている状況を考えます.
で等速直線運動をしている状況を考えます.![]() の
の ![]() 軸に沿って置かれている長さ
軸に沿って置かれている長さ ![]() の棒を,
の棒を,
![]() において同時刻に観測する場合を考察します.(同時刻の設定方法は,前述のフラッシュを使う方法です.)この場合,棒は
において同時刻に観測する場合を考察します.(同時刻の設定方法は,前述のフラッシュを使う方法です.)この場合,棒は ![]() に対して固定されていますので,
に対して固定されていますので,![]() が固有空間の長さになります.
が固有空間の長さになります.![]() における棒の両端の
における棒の両端の ![]() 座標を
座標を
![]() とし,棒の両端の
とし,棒の両端の ![]() 座標を
座標を
![]() における同時刻
における同時刻 ![]() のとき,
のとき,
![]() とします.
とします.
![]() における,この2つの事象を
における,この2つの事象を
![]() とします.これらを
とします.これらを ![]() から見ると,
から見ると,
![]() となります.
となります.
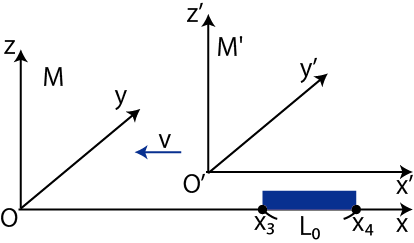
Figure3.14: 空間の収縮3
ここで,Lorentz逆変換の ![]() 成分の式,
成分の式,
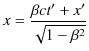
より,
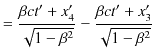 |
||
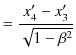 |
となります.ここで,
![]() は
は
![]() での棒の長さを表しますが,これを
での棒の長さを表しますが,これを ![]() とおきます.このとき,
とおきます.このとき,
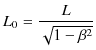 |
||
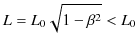 |
となります.つまり,慣性系
![]() から観測した棒の長さ
から観測した棒の長さ ![]() は,
は,![]() での長さ
での長さ ![]() より短いという結論になります.この場合の2次元時空図も記載しておきます.
より短いという結論になります.この場合の2次元時空図も記載しておきます.
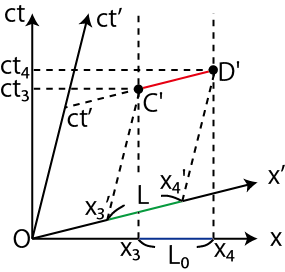
Figure3.15: 空間の収縮4
事象 ![]() と
と ![]() は違いますので,主張の相違があっても問題はありません.Section 前半の議論で出てきた不等式と比較するため,
は違いますので,主張の相違があっても問題はありません.Section 前半の議論で出てきた不等式と比較するため,
![]() としてみましょう.このとき,
としてみましょう.このとき,
となっていて矛盾していません.
3.5 速度の合成則
慣性系間の速度の合成の問題を考えましょう.つまり,慣性系
![]() に対して,速さ
に対して,速さ ![]() で
で ![]() 方向に等速直線運動する慣性系
方向に等速直線運動する慣性系
![]() があり,この
があり,この
![]() に対して速度
に対して速度
![]() で運動する物体があるとします.このとき,
で運動する物体があるとします.このとき,
![]() に対して物体はどのような合成速度
に対して物体はどのような合成速度
![]() で動くかという問題を取り扱います.この場合,Newton力学での結論は,
で動くかという問題を取り扱います.この場合,Newton力学での結論は,
となります.特殊相対性理論の場合,正しい速度の合成則はどのようになるでしょうか? Lorentz変換によって計算していきましょう.
慣性系
![]() に対する物体の速度
に対する物体の速度
![]() を表しましょう.
を表しましょう.
![]() に対する微小時間
に対する微小時間 ![]() の間に,
の間に,
![]() に対する微小変位を
に対する微小変位を
![]() とします.このとき,
とします.このとき,
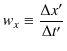 |
||
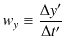 |
||
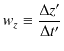 |
と定義されます.この微小変位
![]() を,
を,
![]() から観測することを考えましょう.
から観測することを考えましょう.
![]() と
と
![]() の間のLorentz逆変換の式は次の通りでした.
の間のLorentz逆変換の式は次の通りでした.
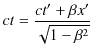 |
||
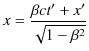 |
||
したがって,これらの微小量は,
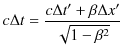 |
||
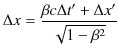 |
||
となります.時間成分は,さらに,
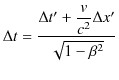
としておきます.ここで,
![]() に対する合成速度
に対する合成速度
![]() は,
は,
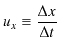 |
||
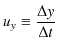 |
||
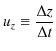 |
と定義されますから,上の微小量を代入して計算します.![]() 成分は,
成分は,
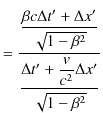 |
||
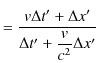 |
||
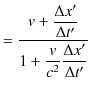 |
ですから,
が成立します.![]() 成分は,
成分は,
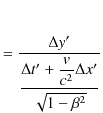 |
||
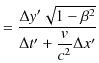 |
||
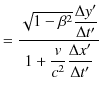 |
||
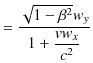 |
と変換されます.![]() 成分も同様の計算により,
成分も同様の計算により,
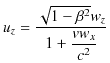
と変換されることがわかります.(上記の議論では,微小量
![]() 等を考えましたが,無限小の極限をとり,
等を考えましたが,無限小の極限をとり,
![]() 等を用いても,同様の関係を導くことができます.)Newton力学では速度の合成則は
等を用いても,同様の関係を導くことができます.)Newton力学では速度の合成則は ![]() 成分については,
成分については,
![]() でしたが,特殊相対性理論では全く異なる結果(3.1)式になります.(
でしたが,特殊相対性理論では全く異なる結果(3.1)式になります.(![]() 成分も変換されます.)この結果を利用すると,特殊相対性理論においては光速以上の速度で運動する慣性系は存在しないということが,重要な結論として導かれます.例えば,
成分も変換されます.)この結果を利用すると,特殊相対性理論においては光速以上の速度で運動する慣性系は存在しないということが,重要な結論として導かれます.例えば,![]() としてみます.このとき,
としてみます.このとき,![]() は次のように(3.1)式を用いて計算されます.
は次のように(3.1)式を用いて計算されます.
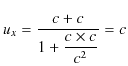
このことは,速度 ![]() と同じ向きの速度
と同じ向きの速度 ![]() を合成すると,
を合成すると,![]() ではなく
ではなく ![]() となることを意味します.常識には反しますが,これも特殊相対性理論の1つの結論です.(
となることを意味します.常識には反しますが,これも特殊相対性理論の1つの結論です.(![]() や
や ![]() が,光速に比べて無視できる場合は,(3.1)式の分母第2項が 0 になりますので,
が,光速に比べて無視できる場合は,(3.1)式の分母第2項が 0 になりますので,
![]() というNewton力学の結論と一致します.)
というNewton力学の結論と一致します.)
同時性の問題,時間の遅れ,双子のparadox,空間の収縮,速度の合成則といった特殊相対性理論の結論は受け入れ難いかもしれません.しかし,このような結論が目に見える効果として現れるのは,運動の速さが光速に対して無視できない程度になった場合です.例としては,高energy加速器や宇宙線などが挙げられますが,特殊相対性理論の結論が正しいことが確認されています.