Chapter6 特殊相対論的力学

6.1 Newton力学

Newton力学の根幹を成す方程式は，次の運動方程式です．

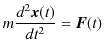
$\displaystyle m\dfrac{d^{2}\bm{x}(t)}{dt^{2}}=\bm{F}(t)$

運動方程式はGalilei変換，

  $\displaystyle t'=t$    
  $\displaystyle x'=x-vt$    
  $\displaystyle y'=y$    
  $\displaystyle z'=z$    

のもとで共変でした．つまり，

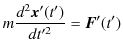
$\displaystyle m\dfrac{d^{2}\bm{x}'(t')}{dt'^{2}}=\bm{F}'(t')$

が成立しました．一方，運動方程式はLorentz変換のもとで共変ではありません．従って，力学は特殊相対性原理の要請を満たし，Lorentz変換に対して共変であるように，修正しなければなりません．（単なる変形ではなく，理論をつくり直すのです．）Lorentz共変性が明白に表されるような力学を構築するためには，4次元的に定式化する必要があります．

 

6.2 固有時間

"特殊相対性理論の世界" のChapterで固有時間という概念を導入しました．固有時間とは，ある慣性系に対して静止している時計によって観測される時間で，その慣性系を等速直線運動していると観測する慣性系で計る時間よりもゆっくりと経過しました．ある慣性系に乗り込んだとき，微小intervalの2乗の式，

$\displaystyle \Delta s^{2}=c^{2}\Delta t^{2}-\Delta x^{2}-\Delta y^{2}-\Delta z^{2}$

において，

  $\displaystyle \Delta t=\Delta\tau$    
  $\displaystyle \Delta x=\Delta y=\Delta z=0$    

が成立します．（ただし，$ \tau$（タウ）は固有時間を強調して表しています．）従って，

$\displaystyle \Delta s(\tau)^{2}=c^{2}\Delta\tau^{2}$

が成り立ちます．また，次の関係式が成立します．

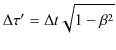
$\displaystyle \Delta\tau'=\Delta t\sqrt{1-\beta^{2}}$

ただし，慣性系 $ M(ct,x,y,z)$ に対して等速直線運動している慣性系 $ M'(ct',x',y',z')$ を考え， $ M'(ct',x',y',z')$ に対する固有時間を問題にしています．導出は次の通りです．

  $\displaystyle \Delta s'(\tau')^{2}=\Delta s(ct,x,y,z)^{2}$    
% latex2html id marker 520 $\displaystyle \therefore$ $\displaystyle c^{2}\Delta\tau'^{2}=c^{2}\Delta t^{2}-\Delta x^{2}-\Delta y^{2}-\Delta z^{2}$    
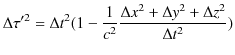% latex2html id marker 522 $\displaystyle \therefore$ $\displaystyle \Delta\tau'^{2}=\Delta t^{2}(1-\dfrac{1}{c^{2}}\dfrac{\Delta x^{2}+\Delta y^{2}+\Delta z^{2}}{\Delta t^{2}})$    
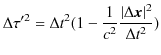% latex2html id marker 524 $\displaystyle \therefore$ $\displaystyle \Delta\tau'^{2}=\Delta t^{2}(1-\dfrac{1}{c^{2}}\dfrac{\vert\Delta\bm{x}\vert^{2}}{\Delta t^{2}})$    
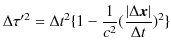% latex2html id marker 526 $\displaystyle \therefore$ $\displaystyle \Delta\tau'^{2}=\Delta t^{2}\{1-\dfrac{1}{c^{2}}(\dfrac{\vert\Delta\bm{x}\vert}{\Delta t})^{2}\}$    
% latex2html id marker 528 $\displaystyle \therefore$ $\displaystyle \Delta\tau'^{2}=\Delta t^{2}(1-\beta^{2})$    
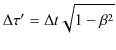% latex2html id marker 530 $\displaystyle \therefore$ $\displaystyle \Delta\tau'=\Delta t\sqrt{1-\beta^{2}}$    

（証明終．）

 

6.3 特殊相対論的力学のLorentz共変性

固有時間を利用して，4元速度vectorを定義します．

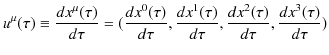  $\displaystyle u^{\mu}(\tau)\equiv\dfrac{dx^{\mu}(\tau)}{d\tau}=(\dfrac{dx^{0}(\... ...c{dx^{1}(\tau)}{d\tau},\dfrac{dx^{2}(\tau)}{d\tau},\dfrac{dx^{3}(\tau)}{d\tau})$    
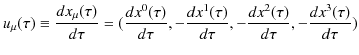  $\displaystyle u_{\mu}(\tau)\equiv\dfrac{dx_{\mu}(\tau)}{d\tau}=(\dfrac{dx^{0}(\... ...dx^{1}(\tau)}{d\tau},-\dfrac{dx^{2}(\tau)}{d\tau},-\dfrac{dx^{3}(\tau)}{d\tau})$    

この4元速度vectorを使って，4元運動量vectorを定義します．

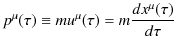  $\displaystyle p^{\mu}(\tau)\equiv mu^{\mu}(\tau)=m\dfrac{dx^{\mu}(\tau)}{d\tau}$    
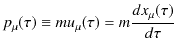  $\displaystyle p_{\mu}(\tau)\equiv mu_{\mu}(\tau)=m\dfrac{dx_{\mu}(\tau)}{d\tau}$    

さらに，4元力を次のように表しておきます．

  $\displaystyle f^{\mu}(\tau)\equiv(0,f^{1}(\tau),f^{2}(\tau),f^{3}(\tau))=(0,f_{x}(\tau),f_{y}(\tau),f_{z}(\tau))$    
  $\displaystyle f_{\mu}(\tau)\equiv(0,f_{1}(\tau),f_{2}(\tau),f_{3}(\tau))=(0,-f_{x}(\tau),-f_{y}(\tau),-f_{z}(\tau))$    

このとき，運動方程式は次のように修正されます．

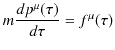  $\displaystyle m\dfrac{dp^{\mu}(\tau)}{d\tau}=f^{\mu}(\tau)$    
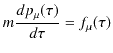  $\displaystyle m\dfrac{dp_{\mu}(\tau)}{d\tau}=f_{\mu}(\tau)$    

このように，運動方程式は4元vectorで表せました．従って，明らかなLorentz共変性をもつことになります．これで，Newton力学は特殊相対性原理の要請を満たすように修正されたことになります．

 

6.4 Lorentz不変量

一般に，ある変換に対して物理量が変化しないとき，物理量は不変性をもつといいます．Lorentz不変量として，2つの4元運動量vectorの縮約からつくられる量を取り上げます．

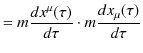$\displaystyle p^{\mu}(\tau)p_{\mu}(\tau)$ $\displaystyle =m\dfrac{dx^{\mu}(\tau)}{d\tau}\cdot m\dfrac{dx_{\mu}(\tau)}{d\tau}$    
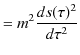  $\displaystyle =m^{2}\dfrac{ds(\tau)^{2}}{d\tau^{2}}$    
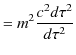  $\displaystyle =m^{2}\dfrac{c^{2}d\tau^{2}}{d\tau^{2}}$    
  $\displaystyle =m^{2}c^{2}$    

故に，

$\displaystyle p^{\mu}(\tau)p_{\mu}(\tau)=m^{2}c^{2}$ (6.1)

が成立します．また，4元運動量の第0成分でenergyを定義します．

$\displaystyle E\equiv cp^{0}$

このとき，(6.1)式より，

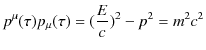
$\displaystyle p^{\mu}(\tau)p_{\mu}(\tau)=(\dfrac{E}{c})^{2}-p^{2}=m^{2}c^{2}$

となります．ただし，$ p$ は4元運動量vectorの空間成分の大きさで，

$\displaystyle p\equiv\vert\bm{p}\vert$

を意味します．このとき，

$\displaystyle E^{2}=c^{2}p^{2}+m^{2}c^{4}$ (6.2)

が成立します．特に，(6.2)式で $ p=0$ を代入すると，有名な静止energyの式，

$\displaystyle E=mc^{2}$ (6.3)

が成立します．(6.2)式を変形すると，

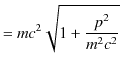$\displaystyle E$ $\displaystyle =mc^{2}\sqrt{1+\dfrac{p^{2}}{m^{2}c^{2}}}$    
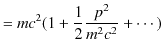  $\displaystyle =mc^{2}(1+\dfrac{1}{2}\dfrac{p^{2}}{m^{2}c^{2}}+\cdots)$    
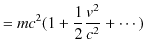  $\displaystyle = mc^{2}(1+\dfrac{1}{2}\dfrac{v^{2}}{c^{2}}+\cdots)$    
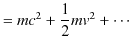  $\displaystyle =mc^{2}+\dfrac{1}{2}mv^{2}+\cdots$    

となりますが，第1項が静止energyで，第2項がNewton力学の運動energyを表します．(6.3)式は，質量はenergyであるという意味をもち，原子力energy等に応用されています．