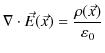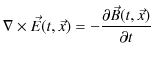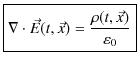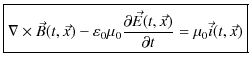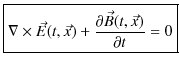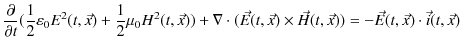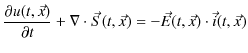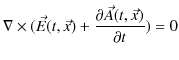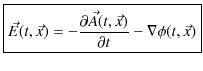J Simplicity マクスウェル方程式

J Simplicity

Part2 電磁気学の成立

Chapter13 マクスウェル方程式

13.1 マクスウェル方程式

いままでのChapterに出てきた電場と磁場に関する法則の微分形の方程式を再掲します．まず，静電場に関するガウスの法則，

$\displaystyle \nabla\cdot\vec{E}(\vec{x})=\dfrac{\rho(\vec{x})}{\varepsilon_{0}}$

(13.1)

と，静磁場に関するガウスの法則，

$\displaystyle \nabla\cdot\vec{B}(\vec{x})=0$

(13.2)

が成立します．そして，電場と磁場の間に成立する法則は2つあります．定常電流がつくる静磁場についてのアンペールの法則，

$\displaystyle \nabla\times\vec{B}(\vec{x})=\mu_{0}\vec{i}(\vec{x})$

(13.3)

と，ファラデーの電磁誘導の法則，

$\displaystyle \nabla\times\vec{E}(t,\vec{x})=-\dfrac{\partial\vec{B}(t,\vec{x})}{\partial t}$

(13.4)

です．(13.4)式は時間的変化に関しても含んだ方程式になっています．残りの３式も時間的変化を取り入れた方程式に修正しましょう．静電場と静磁場に関するガウスの法則(13.1)式と(13.2)式は，そのままの形で時間的に変動する電場，磁場の場合に拡張できるものとします．すなわち，

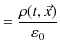$\displaystyle \nabla\cdot\vec{E}(t,\vec{x})$	$\displaystyle =\dfrac{\rho(t,\vec{x})}{\varepsilon_{0}}$
$\displaystyle \nabla\cdot\vec{B}(t,\vec{x})$	$\displaystyle =0$

とします．

　ここで，アンペールの法則(13.3)式を修正する準備をしておきます．電流保存則（積分形）は，

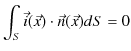
$\displaystyle \int_{S}\vec{i}(\vec{x})\cdot\vec{n}(\vec{x})dS=0$

でした．この法則は定常電流に対して成立するものです．電気の流れが定常的ではなく，面から流失する電荷が正の値をもつとき，の内部にある電荷の値は減少します．その単位時間当たりの減少量は， $-\frac{dQ}{dt}$ で与えられるので，上の電流保存則の代わりに，電荷保存則（積分形），

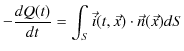
$\displaystyle -\dfrac{dQ(t)}{dt}=\int_{S}\vec{i}(t,\vec{x})\cdot\vec{n}(\vec{x})dS$

が成り立ちます．ここで，電荷は電荷密度 $\rho[C/m^{3}]$ を使って，

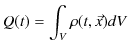
$\displaystyle Q(t)=\int_{V}\rho(t,\vec{x})dV$

と体積分で表せます．また，ベクトル解析のガウスの定理，

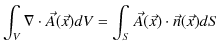
$\displaystyle \int_{V}\nabla\cdot\vec{A}(\vec{x})dV=\int_{S}\vec{A}(\vec{x})\cdot\vec{n}(\vec{x})dS$

が成立しますので，面積分を体積分で表すことができます．したがって，電荷保存則は，次のように変形できます．

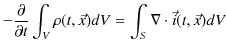	$\displaystyle -\dfrac{\partial}{\partial t}\int_{V}\rho(t,\vec{x})dV=\int_{S}\nabla\cdot\vec{i}(t,\vec{x})dV$
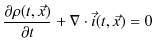$% latex2html id marker 1189 $\displaystyle \therefore$$	$\displaystyle \dfrac{\partial\rho(t,\vec{x})}{\partial t}+\nabla\cdot\vec{i}(t,\vec{x})=0$

最後の式が電荷保存則（微分形）であり，連続の方程式ともいいます．

　話をもとに戻して，アンペールの法則(13.3)式に時間変化を取り入れて拡張しましょう．そのままの形で拡張すると，

$\displaystyle \nabla\times\vec{B}(t,\vec{x})=\mu_{0}\vec{i}(t,\vec{x})$

となります．ここで，この式の両辺の発散をとると，

$\displaystyle \nabla\cdot\nabla\times\vec{B}(t,\vec{x})=\mu_{0}\nabla\cdot\vec{i}(t,\vec{x})$

となりますが，左辺はベクトル解析の公式，

$\displaystyle \nabla\cdot\nabla\times\vec{A}(\vec{x})=0$

より，恒等的に0になります．したがって，

$\displaystyle \nabla\cdot\vec{i}(t,\vec{x})=0$

となりますが，この式は定常電流の保存則です．しかし，電荷密度と電流密度が時間的に変化する場合は，電荷保存則である連続の方程式，

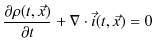
$\displaystyle \dfrac{\partial\rho(t,\vec{x})}{\partial t}+\nabla\cdot\vec{i}(t,\vec{x})=0$

が成立しなければなりません．そこで，ここが肝心なところですが，マクスウェルは方程式に変位電流と呼ばれるものを付け加えて，次のようにアンペールの法則を修正しました．

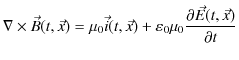
$\displaystyle \nabla\times\vec{B}(t,\vec{x})=\mu_{0}\vec{i}(t,\vec{x})+\varepsilon_{0}\mu_{0}\dfrac{\partial\vec{E}(t,\vec{x})}{\partial t}$

このとき，両辺の発散をとると，

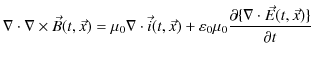	$\displaystyle \nabla\cdot\nabla\times\vec{B}(t,\vec{x})=\mu_{0}\nabla\cdot\vec{... ...epsilon_{0}\mu_{0}\dfrac{\partial\{\nabla\cdot\vec{E}(t,\vec{x})\}}{\partial t}$
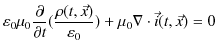$% latex2html id marker 1204 $\displaystyle \therefore$$	$\displaystyle \varepsilon_{0}\mu_{0}\dfrac{\partial}{\partial t}(\dfrac{\rho(t,\vec{x})}{\varepsilon_{0}})+\mu_{0}\nabla\cdot\vec{i}(t,\vec{x})=0$
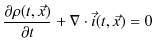$% latex2html id marker 1206 $\displaystyle \therefore$$	$\displaystyle \dfrac{\partial\rho(t,\vec{x})}{\partial t}+\nabla\cdot\vec{i}(t,\vec{x})=0$

となり，連続の方程式が成立します．以上で，電磁気学の基礎方程式である4式からなるマクスウェル方程式が揃いました．まとめておきましょう．

$\displaystyle \fbox{$\nabla\cdot\vec{E}(t,\vec{x})=\dfrac{\rho(t,\vec{x})}{\varepsilon_{0}}$}$

(13.5)

$\displaystyle \fbox{$\nabla\cdot\vec{B}(t,\vec{x})=0$}$

(13.6)

$\displaystyle \fbox{$\nabla\times\vec{B}(t,\vec{x})-\varepsilon_{0}\mu_{0}\dfrac{\partial\vec{E}(t,\vec{x})}{\partial t}=\mu_{0}\vec{i}(t,\vec{x})$}$

(13.7)

$\displaystyle \fbox{$\nabla\times\vec{E}(t,\vec{x})+\dfrac{\partial\vec{B}(t,\vec{x})}{\partial t}=0$}$

(13.8)

また，電場と磁場が存在するとき，運動する荷電粒子が受ける力は，"アンペール力とローレンツ力" のChapterより，

$\displaystyle \fbox{$\vec{F}=q\vec{E}+q\vec{v}\times\vec{B}$}$

(13.9)

で表されました．(13.5)式，(13.6)式，(13.7)式，(13.8)式のマクスウェル方程式４式と(13.9)式の合計５式が電磁気学の根幹を成しています．

13.2 電磁場のエネルギー

電磁場のエネルギーについて，考えてみましょう．まず， $\vec{E}(t,\vec{x})[N/C]$ と(13.7)式， $\vec{B}(t,\vec{x})[T]$ と(13.8)式のスカラー積を，それぞれつくると，

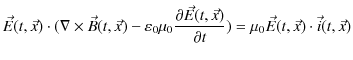	$\displaystyle \vec{E}(t,\vec{x})\cdot(\nabla\times\vec{B}(t,\vec{x})-\varepsilo... ...ec{E}(t,\vec{x})}{\partial t})=\mu_{0}\vec{E}(t,\vec{x})\cdot\vec{i}(t,\vec{x})$
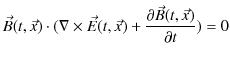	$\displaystyle \vec{B}(t,\vec{x})\cdot(\nabla\times\vec{E}(t,\vec{x})+\dfrac{\partial\vec{B}(t,\vec{x})}{\partial t})=0$

を得ます．下の式から上の式を辺々引いて計算すると，

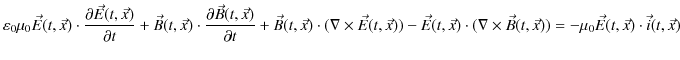	$\displaystyle \varepsilon_{0}\mu_{0}\vec{E}(t,\vec{x})\cdot\dfrac{\partial\vec{... ...abla\times\vec{B}(t,\vec{x}))=-\mu_{0}\vec{E}(t,\vec{x})\cdot\vec{i}(t,\vec{x})$
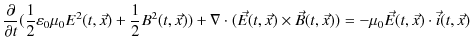$% latex2html id marker 1226 $\displaystyle \therefore$$	$\displaystyle \dfrac{\partial}{\partial t}(\dfrac{1}{2}\varepsilon_{0}\mu_{0}E^... ...{x})\times\vec{B}(t,\vec{x}))=-\mu_{0}\vec{E}(t,\vec{x})\cdot\vec{i}(t,\vec{x})$

ですから，

$\displaystyle \dfrac{\partial}{\partial t}(\dfrac{1}{2}\varepsilon_{0}E^{2}(t,\... ...(t,\vec{x})\times\vec{H}(t,\vec{x}))=-\vec{E}(t,\vec{x})\cdot\vec{i}(t,\vec{x})$

(13.10)

が得られます．ただし，ベクトル解析の公式，

$\displaystyle \nabla\times(\vec{A}\times\vec{B})=\vec{B}\cdot(\nabla\times\vec{A})-\vec{A}\cdot(\nabla\times\vec{B})$

と，

$\displaystyle \vec{B}(t,\vec{x})=\mu_{0}\vec{H}(t,\vec{x})$

の関係式を用いました．ここで，次の２つの量を定義します．

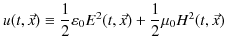	$\displaystyle u(t,\vec{x})\equiv\dfrac{1}{2}\varepsilon_{0}E^{2}(t,\vec{x})+\dfrac{1}{2}\mu_{0}H^{2}(t,\vec{x})$
	$\displaystyle \vec{S}(t,\vec{x})\equiv\vec{E}(t,\vec{x})\times\vec{H}(t,\vec{x})$

このとき，(13.10)式は，

$\displaystyle \dfrac{\partial u(t,\vec{x})}{\partial t}+\nabla\cdot\vec{S}(t,\vec{x})=-\vec{E}(t,\vec{x})\cdot\vec{i}(t,\vec{x})$

(13.11)

となります．この(13.11)式は連続の方程式とよく似た形をしていますが，Balance方程式といいます．そして，次のように解釈できます．右辺の $\vec{E}(t,\vec{x})\cdot\vec{i}(t,\vec{x})[J/m^{3}\cdot s]$ は，単位体積中の荷電粒子が，電場から受ける単位時間当たりの仕事でした．磁場が存在していても，ローレンツ力は荷電粒子の運動の向きに垂直に働くので，荷電粒子は磁場から仕事をされません．したがって，右辺の量は電磁場が荷電粒子に仕事をした分だけ減少するものです．そして，電磁場が荷電粒子に仕事をした分だけ減少するものは，電磁場のエネルギーです．故に， $u(t,\vec{x})[J/m^{3}]$ は電磁場のエネルギー密度， $\vec{S}(t,\vec{x})[J/m^{2}\cdot s]$ は電磁場のエネルギー密度の流れを表すベクトル（ポインティングベクトルといいます．）と定義することができます．上記の(13.11)式は電磁場のエネルギー保存則を表しています．

13.3 電磁ポテンシャル

マクスウェル方程式をもう少し見やすい形に変形しておきましょう．そのために電磁ポテンシャルといわれるものを導入します．まず，静電場の場合，"静電位" のChapterで出てきた，

$\displaystyle \vec{E}(\vec{x})=-\nabla\phi(\vec{x})$

が成立します．つまり，静電場はスカラー・ポテンシャル（電位） $\phi(\vec{x})$ によって表すことができます．また，静磁場の場合には，ガウスの法則（微分形），

$\displaystyle \nabla\cdot\vec{B}(\vec{x})=0$

(13.12)

が成立します．ここで，任意のベクトル関数 $\vec{A}(\vec{x})$ を導入して，

$\displaystyle \vec{B}(\vec{x})=\nabla\times\vec{A}(\vec{x})$

より，常に(13.12)式が成立することが保証されます． $\vec{A}(\vec{x})$ をベクトル・ポテンシャルといいます．スカラー・ポテンシャルとベクトル・ポテンシャルを併せて電磁ポテンシャルといいます．

　それでは，時間的に変動する一般の電磁場の場合は，どのようになるのでしょうか？磁場に関しては，ガウスの法則（微分形）(13.12)式を拡張したマクスウェル方程式の第2式である(13.6)式，

$\displaystyle \nabla\cdot\vec{B}(t,\vec{x})=0$

が成立しましたので，

$\displaystyle \fbox{$\vec{B}(t,\vec{x})=\nabla\times\vec{A}(t,\vec{x})$}$

(13.13)

となります．時間依存性を含む場合，電場については，ファラデーの電磁誘導の法則，すなわち，マクスウェル方程式の第4式である(13.8)式，

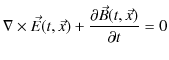
$\displaystyle \nabla\times\vec{E}(t,\vec{x})+\dfrac{\partial\vec{B}(t,\vec{x})}{\partial t}=0$

が成立しました．左辺第２項が 0 でないため，電場をスカラー・ポテンシャルのみで表すことは不可能です．そこで，先程の(13.13)式を，左辺第２項に代入して計算します．

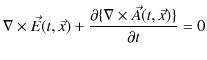
$\displaystyle \nabla\times\vec{E}(t,\vec{x})+\dfrac{\partial\{\nabla\times\vec{A}(t,\vec{x})\}}{\partial t}=0$

ですから，

$\displaystyle \nabla\times(\vec{E}(t,\vec{x})+\dfrac{\partial\vec{A}(t,\vec{x})}{\partial t})=0$

(13.14)

となります．ここで，

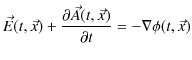
$\displaystyle \vec{E}(t,\vec{x})+\dfrac{\partial\vec{A}(t,\vec{x})}{\partial t}=-\nabla\phi(t,\vec{x})$

とおき，新たなスカラー・ポテンシャル $\phi(t,\vec{x})$ を導入すると，ベクトル解析の公式，

$\displaystyle \nabla\times(\nabla\phi)=0$

より，(13.14)式が成立することが保証されます．よって，時間的に変動する電場は，次式で表されます．

$\displaystyle \fbox{$\vec{E}(t,\vec{x})=-\dfrac{\partial\vec{A}(t,\vec{x})}{\partial t}-\nabla\phi(t,\vec{x})$}$

(13.15)

13.4 物理量と単位の定義

いままでのChapterに出てきた電磁気学の物理量と単位についてまとめておきます．電磁気学ではMKSA単位系を採用します．すなわち，長さの単位に，質量の単位に，時間の単位に，電流の単位にを使います．その中の電流の単位の定義から始めましょう．そのために，平行電流間に働き合う力を考えます．1本の電流を $I_{1}[A]$ ，もう1本の電流を $I_{2}[A]$ とします．電流間の距離をとすると，働き合う力の大きさは，

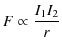
$\displaystyle F\propto\dfrac{I_{1}I_{2}}{r}$

ですので，導線あたりに働き合う力の大きさを，

$\displaystyle F[N/m]=2.0\times10^{-7}[N/A^{2}]\times\dfrac{I_{1}[A]I_{2}[A]}{r[m]}$

と表し，電流の単位を定義します．つまり，とは真空中で隔てて平行に置かれた2本の導線に同じ強さの電流を流したとき，導線同士が及ぼしあう力の大きさがあたり， $2.0\times10^{-7}[N]$ のときの電流の強さとします．電流の単位が定義されたので，これから電荷の単位を定義します．より，

$\displaystyle 1[C]=1[A]\times1[s]$

と決定されます．

　次に，導線 $\ell[m]$ 当たりに電流 $I_{1}[A]$ に働く力を，電流 $I_{2}[A]$ がつくる磁場で表してみると，

$\displaystyle F[N]$	$\displaystyle =2.0\times10^{-7}[N/A^{2}]\times\dfrac{I_{1}[A]I_{2}[A]}{r[m]}\times\ell[m]$
	$\displaystyle =I_{1}[A]\times4\pi\times10^{-7}[N/A^{2}]\times\dfrac{I_{2}[A]}{2\pi r[m]}\times\ell[m]$
	$\displaystyle =I_{1}[A]\times\mu_{0}[N/A^{2}]H[A/m]\times\ell[m]$

となります．ただし，

$\displaystyle \mu_{0}\equiv4\pi\times10^{-7}[N/A^{2}]$

と真空の透磁率を定義しました．さらに，上式を，

$\displaystyle F=IB\ell$

と変形し，磁束密度を次式で定義します．つまり，

$\displaystyle B[T]=\mu_{0}[N/A^{2}]H[A/m]$

となります．ここで，

$\displaystyle [T]=[N/A\cdot m]$

の関係があることがわかります．

　それから，磁気力に関しては，

$\displaystyle F\propto\dfrac{m_{1}m_{2}}{r^{2}}$

が成立します．ここで，電荷に関するクーロンの法則，

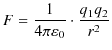
$\displaystyle F=\dfrac{1}{4\pi\varepsilon_{0}}\cdot\dfrac{q_{1}q_{2}}{r^{2}}$

に合わせて，磁気力を，

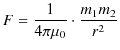
$\displaystyle F=\dfrac{1}{4\pi\mu_{0}}\cdot\dfrac{m_{1}m_{2}}{r^{2}}$

と表し，磁荷を定義します．このとき，

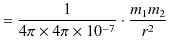$\displaystyle F$	$\displaystyle =\dfrac{1}{4\pi\times4\pi\times10^{-7}}\cdot\dfrac{m_{1}m_{2}}{r^{2}}$
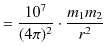	$\displaystyle =\dfrac{10^{7}}{(4\pi)^{2}}\cdot\dfrac{m_{1}m_{2}}{r^{2}}$

となります．

　磁荷の単位と磁束の単位が同じになることも確認しておきましょう．

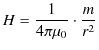
$\displaystyle H=\dfrac{1}{4\pi\mu_{0}}\cdot\dfrac{m}{r^{2}}$

より，

$\displaystyle m$	$\displaystyle =4\pi\mu_{0}r^{2}H$
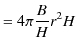	$\displaystyle =4\pi\dfrac{B}{H}r^{2}H$
	$\displaystyle =4\pi Br^{2}$

です．故に，磁荷の単位は，

$\displaystyle [Wb]=[T][m^{2}]$

となります．これは確かに，磁束 $\Phi=BS$ の単位と一致します．