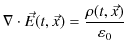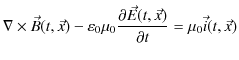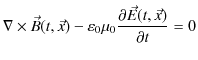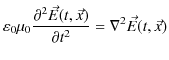Chapter14 電磁波
14.1 電磁波
前のChapterで見たように,電磁気学の根幹をなすマクスウェル方程式とは次の4式のことです.
ここで,電荷密度
![]() と電流密度
と電流密度
![]() が 0 であるような真空の空間領域を考え,その領域で起こる現象を調べましょう.このとき,マクスウェル方程式は次のようになります.
が 0 であるような真空の空間領域を考え,その領域で起こる現象を調べましょう.このとき,マクスウェル方程式は次のようになります.
それでは,電場
![]() の満たす方程式を導きましょう.(14.8)式に左から
の満たす方程式を導きましょう.(14.8)式に左から
![]() を掛けます.(回転をとります.)
を掛けます.(回転をとります.)
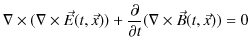
ここで,ベクトル解析の公式,
より,
ですが,ここで,(14.5)式より,
となります.さらに,(14.7)式より,
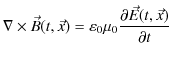
となります.故に,
![]() の満たす方程式は,
の満たす方程式は,
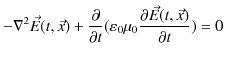
ですから,
となります.次に,磁束密度
![]() の満たす方程式を導きましょう.(14.7)式に左から
の満たす方程式を導きましょう.(14.7)式に左から
![]() を掛けます.(回転をとります.)
を掛けます.(回転をとります.)
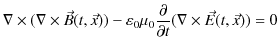
ここで,ベクトル解析の公式,
より,
ですが,ここで,(14.6)式より,
となります.さらに,(14.8)式より,
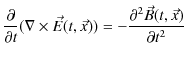
となります.故に,
![]() の満たす方程式は,
の満たす方程式は,
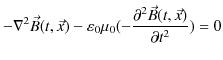
ですから,
となります.
ここで,(14.9)式と(14.10)式は,3次元波動方程式,
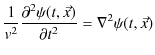
と同じ形をしていることに注意しましょう.(ただし,![]() は波動の伝搬速度の大きさ,
は波動の伝搬速度の大きさ,
![]() は波動のもつ一般量です.)つまり,電場
は波動のもつ一般量です.)つまり,電場
![]() と磁束密度
と磁束密度
![]() は,波動として空間に対して時間的に伝搬するのです.この波動のことを電磁波といいます.さらに,その伝搬の速さ
は,波動として空間に対して時間的に伝搬するのです.この波動のことを電磁波といいます.さらに,その伝搬の速さ ![]() は,(14.9)式と(14.10)式を波動方程式と比較することにより,次のように求められます.
は,(14.9)式と(14.10)式を波動方程式と比較することにより,次のように求められます.
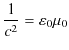
ですから,
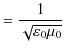 |
||
![$\displaystyle =\dfrac{1}{\sqrt{8.8541878\times10^{-12}[F/m]\times4\pi(=3.14159265)\times10^{-7}[N/A^{2}]}}$](ja_Chapter14_ElectromagneticWave_images/img32.png) |
||
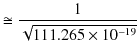 |
||
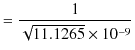 |
||
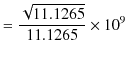 |
||
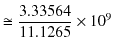 |
||
です.この数値は光速の測定値,
と完全に一致します.もっとも,現代では,真空の誘電率
![]() は光速
は光速 ![]() から計算するので,この完全な一致は当然です.しかし,その当時,光速と電磁波の伝搬速度の一致は予測できなかったもので,光が電磁波であることの確固たる証拠となりました.この偉大な発見は物理学の勝利の一つと言えるでしょう.また,光が電磁波であることは特殊相対性理論の理論的基礎となっています.
から計算するので,この完全な一致は当然です.しかし,その当時,光速と電磁波の伝搬速度の一致は予測できなかったもので,光が電磁波であることの確固たる証拠となりました.この偉大な発見は物理学の勝利の一つと言えるでしょう.また,光が電磁波であることは特殊相対性理論の理論的基礎となっています.
電場
![]() と磁束密度
と磁束密度
![]() の具体的な1つの解としては,波動方程式の一般論に従い,正弦波を挙げることができます.電場については,
の具体的な1つの解としては,波動方程式の一般論に従い,正弦波を挙げることができます.電場については,
であり,磁束密度については,
です.電場
![]() と磁束密度
と磁束密度
![]() のそれぞれについて,最初の式が正の方向に伝搬する波動,2番目の式が負の方向に伝搬する波動を表します.以下の議論では,正の方向に伝搬する波動を扱います.負の方向に伝搬する波動についても同様です.
のそれぞれについて,最初の式が正の方向に伝搬する波動,2番目の式が負の方向に伝搬する波動を表します.以下の議論では,正の方向に伝搬する波動を扱います.負の方向に伝搬する波動についても同様です.
![]() と
と ![]() は電場と磁束密度のそれぞれの振幅を,
は電場と磁束密度のそれぞれの振幅を,
![]() と
と
![]() は電場と磁束密度それぞれのベクトルの方向の単位ベクトルを表します.ここで,(14.5)式,
は電場と磁束密度それぞれのベクトルの方向の単位ベクトルを表します.ここで,(14.5)式,
の左辺に,正の方向に伝搬する電場
![]() の表式を代入して計算します.
の表式を代入して計算します.
 |
||
よって,(14.5)式より,
が成立します.同様に,(14.6)式,
の左辺に,正の方向に伝搬する磁束密度 ![]() の表式を代入して計算します.
の表式を代入して計算します.
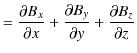 |
||
よって,(14.6)式より,
が成立します.つまり,波動の偏りの方向
![]() と
と
![]() は波動の進行方向
は波動の進行方向
![]() に対して直交しています.すなわち,電磁波は横波であることが証明されました.このことは,先に述べた電磁波の伝搬速度が光速に一致することとともに,光が電磁波であることの証拠となりました.
(14.8)式,
に対して直交しています.すなわち,電磁波は横波であることが証明されました.このことは,先に述べた電磁波の伝搬速度が光速に一致することとともに,光が電磁波であることの証拠となりました.
(14.8)式,
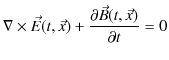
に,正の方向に伝搬する正弦波の式を代入して計算します.
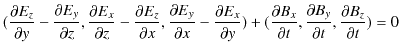 |
||
ここで,伝搬方向に向きをもつ波数ベクトル ![]() の向きの単位ベクトルを,
の向きの単位ベクトルを,
![]() とおきます.このとき,
とおきます.このとき,![]() の大きさを
の大きさを ![]() として,
として,
と表せます.したがって,上の式は,
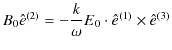 |
||
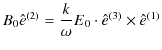 |
となります.さらに,
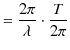 |
||
なので,
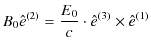
の関係が成立します.この式を,振幅の関係と偏りの関係に分けて書くと次のようになります.
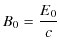 |
||
したがって,電磁波の様子を図に示すと次のようになります.
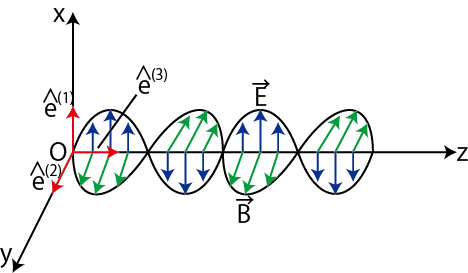
Figure14.1: 電磁波