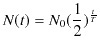Chapter7 量子状態(波動関数と確率振幅)
7.1 量子的事象1(原子核の崩壊)
波動関数とは何でしょうか? 量子的な事象を取り扱い,その物理的意味を考え,量子力学の基礎的な概念と原理を導入することにしましょう.
最初の量子的な事象として,原子核の崩壊というものを見ていくことにします.ある特定の物質が自発的に放射線を出すはたらきを放射能といいます.放射線にはα線,β線,γ線の3つがあります.α線の正体はヘリウムの原子核であり,電離作用が大きく,透過度は小さいという特徴があります.β線の正体は電子であり,電離作用,透過度はともに中程度です.γ線の正体は振動数の大きい電磁波であり,電離作用が小さく,透過度は大きいという特徴があります.放射線が発生するのは,放射性物質の原子核が崩壊し,元素が変換するためです.古来,錬金術の研究が行われた時代がありましたが,原子核の崩壊は現代における錬金術ということが言えるでしょう.α線を放出する崩壊をα崩壊といいます.この過程では原子核からヘリウムの原子核が出るので,次のように表せます.
原子番号 ![]() は
は ![]() 減少し,質量数
減少し,質量数 ![]() は
は ![]() 減少します.
減少します.![]() や
や ![]() は元素の種類を一般的に表しています.元素の種類が変換されています.次に,β線を放出する崩壊であるβ崩壊を考えましょう.この過程では,原子核内部で,
は元素の種類を一般的に表しています.元素の種類が変換されています.次に,β線を放出する崩壊であるβ崩壊を考えましょう.この過程では,原子核内部で,
というように,中性子 ![]() が陽子
が陽子 ![]() ,電子
,電子 ![]() とニュートリノ
とニュートリノ ![]() に変換しています.この結果,元素は次のように変換します.
に変換しています.この結果,元素は次のように変換します.
原子核内部で中性子が陽子になったので,原子番号 ![]() は
は ![]() 増えますが,質量数
増えますが,質量数 ![]() は変化しません.そして,α崩壊またはβ崩壊した直後の不安定な状態にある原子核が,余分なエネルギーを電磁波としてγ線を放出する過程が,γ崩壊です.
は変化しません.そして,α崩壊またはβ崩壊した直後の不安定な状態にある原子核が,余分なエネルギーを電磁波としてγ線を放出する過程が,γ崩壊です.
このように,γ崩壊しても原子番号 ![]() と質量数
と質量数 ![]() は変化せず,元素の種類はもとのままです.γ崩壊は原子核内部の反応なので,放出されるエネルギーが大きく,振動数の高い電磁波が放出されます.このことはアインシュタイン-ド・ブロイの関係式の第1式,
は変化せず,元素の種類はもとのままです.γ崩壊は原子核内部の反応なので,放出されるエネルギーが大きく,振動数の高い電磁波が放出されます.このことはアインシュタイン-ド・ブロイの関係式の第1式,
から理解されます.(原子内部の電子の軌道間の遷移による反応では,放出されるエネルギーがγ崩壊よりも小さく,γ線よりも振動数の低い電磁波である可視光線が放出されることが,よく知られています."原子構造と前期量子論" のChapterを参照して下さい.)
それでは,原子核崩壊のメカニズムについて考えてみましょう.原子核が ![]() と崩壊するとき,原子核
と崩壊するとき,原子核 ![]() の初めの数
の初めの数 ![]() が
が
![]() になるまでの時間,その残りの
になるまでの時間,その残りの ![]() の数
の数
![]() がまた
がまた
![]() になるまでの時間,そのまた残った
になるまでの時間,そのまた残った ![]() の数
の数
![]() がさらに
がさらに
![]() になるまでの時間は全て同じになります.(以下,続く.)このことは,原子核が崩壊する過程が,本質的に確率的なものであることを意味しています.つまり,ある特定の原子核がいつ崩壊するかを決定することは不可能なのです.ここで,もとの原子核が半分になる時間を半減期といい,
になるまでの時間は全て同じになります.(以下,続く.)このことは,原子核が崩壊する過程が,本質的に確率的なものであることを意味しています.つまり,ある特定の原子核がいつ崩壊するかを決定することは不可能なのです.ここで,もとの原子核が半分になる時間を半減期といい,![]() で表します.(もし,決定論的に原子核が崩壊するならば,
で表します.(もし,決定論的に原子核が崩壊するならば,![]() 経過すると,全ての原子核
経過すると,全ての原子核 ![]() が
が ![]() に崩壊してしまうはずですね.)時刻
に崩壊してしまうはずですね.)時刻 ![]() において,残った元素
において,残った元素 ![]() の原子核の個数を
の原子核の個数を ![]() とすると,次式が成立します.
とすると,次式が成立します.
この(7.1)式において,![]() に
に
![]() を代入すると,上記の崩壊の状況が確認されます.
を代入すると,上記の崩壊の状況が確認されます.
さらに,原子核崩壊の問題を微分方程式で取り扱ってみましょう.以下の議論により,原子核崩壊の現象の本質が確率的性質をもっていることが,はっきりと理解されます.1個の原子核が,ある時刻から次の ![]() 秒の間に崩壊する確率を
秒の間に崩壊する確率を ![]() とすれば,
とすれば,![]() 個の原子核の中で,微小時間
個の原子核の中で,微小時間 ![]() 間に
間に
![]() 個だけが崩壊することになります.(
個だけが崩壊することになります.(![]() を崩壊定数といいます.)したがって,
を崩壊定数といいます.)したがって,![]() の変化量
の変化量 ![]() は次のように表されます.
は次のように表されます.
ここで,極限をとると,
となります.両辺を ![]() で割って,
で割って,
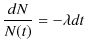
ですが,両辺を不定積分して計算します.
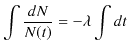 |
||
ただし,![]() は積分定数です.ここで,初期条件として,
は積分定数です.ここで,初期条件として,![]() で元素
で元素 ![]() が
が ![]() 個あったとすると,
個あったとすると,
となるので,
が微分方程式の解になります.(7.1)式と(7.2)式を比較すると,
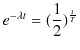
となります.この方程式を解くと,
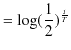 |
||
となり,よって,
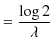 |
||
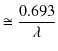 |
の関係があることがわかります.崩壊の過程を確率的であるとした微分方程式による方法が,経験式である(7.1)式を再現することが確認できました.
原子核の崩壊が確率論的に起こるということは,量子力学の本質を表しています.すなわち,ミクロ世界においては,ニュートン力学的な決定論ではなく確率論的な自然法則が支配しているのです.このことの一端を原子核の崩壊現象は示しています.
7.2 量子的事象2(2重スリットの実験)
前のSectionに引き続き,量子的な概念と原理を導入するため,特に波動関数 ![]() の意味を知るため,2重スリットの実験というものを取り扱うことにします.この実験は光についてのヤングの実験としてお馴染みのものです.ヤングの実験の内容は,同位相の光を2重スリットに通すと,スクリーン上に干渉模様が現れ,光の波動性を示すものとして知られています.ここでは,光の代わりに電子を考えてみます.
の意味を知るため,2重スリットの実験というものを取り扱うことにします.この実験は光についてのヤングの実験としてお馴染みのものです.ヤングの実験の内容は,同位相の光を2重スリットに通すと,スクリーン上に干渉模様が現れ,光の波動性を示すものとして知られています.ここでは,光の代わりに電子を考えてみます.
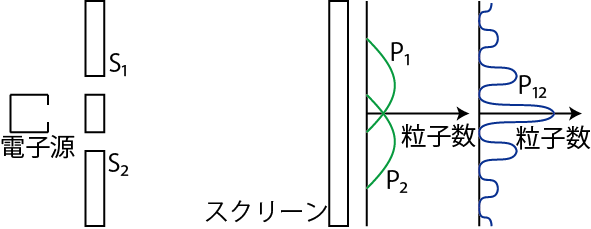
Figure7.1: 2重スリットの実験
実験装置は図の通りです.左にある電子源から電子のビームをスリットに打ち込み,右にあるスクリーン上で電子を観測します.観測される電子は紛れもなく粒子です.この事実は電子の2重性のうちの粒子性を表していると理解できます.ここで,観測される電子の粒子数について考えてみましょう.仮に,スリット ![]() が閉じていて,スリット
が閉じていて,スリット ![]() のみが開いている場合には,粒子数の分布は図の
のみが開いている場合には,粒子数の分布は図の ![]() のようになります.逆に,スリット
のようになります.逆に,スリット ![]() が閉じていて,スリット
が閉じていて,スリット ![]() のみが開いている場合には,粒子数の分布は図の
のみが開いている場合には,粒子数の分布は図の ![]() のようになります.この分布は電子が粒子であるとしても,波動であるとしても同じ結果になります.それでは,2つのスリット
のようになります.この分布は電子が粒子であるとしても,波動であるとしても同じ結果になります.それでは,2つのスリット ![]() とスリット
とスリット ![]() が両方とも開いていたらどうなるでしょうか? もし,粒子数の分布が中央をピークとした1つの山だけのものになった場合は,すなわち,
が両方とも開いていたらどうなるでしょうか? もし,粒子数の分布が中央をピークとした1つの山だけのものになった場合は,すなわち,
となったときには,電子の粒子性が現われていると結論できます.(この粒子数の分布は図には示していません.)しかし,正しい結論はこのようにはなりません.波動力学に従うと,粒子数の分布 ![]() は図に示したように綺麗な干渉模様になります.ここに電子の波動性が現われています.このとき,
は図に示したように綺麗な干渉模様になります.ここに電子の波動性が現われています.このとき,
の関係が成立します.以上の議論により,スリットを通る前,スリットを通るとき,スリットから出てスクリーンに到達するまで,電子は波動として振る舞い,スクリーンで観測されたとき,電子は粒子として存在することが結論付けられます.
では,スクリーン上で観測される前の波動の正体は何でしょうか? さらに問題を深く考えるため,電子のビームの強度を極端に弱くしてみましょう.例えば,電子を1個しか送らなかったとしましょう.当然,スクリーン上には1個の電子しか発見されません.これでは干渉の効果を測定しようがなく,電子の波動性がはっきりとわかりません.しかし,実は,この場合も干渉模様を観測することができます.その方法は,電子を1個ずつ,時間をかけて送り続けるのです.最初はポツリポツリとしか,電子は観測されません.ここで,スクリーンのどの場所に電子が観測されるかを決定することは不可能です.しかし,長時間にわたって観測された電子の粒子数の分布を描いてみれば,見事な干渉模様が現れます.つまり,この場合も電子は1個だけでも,スリットを通る前,スリットを通るとき,スリットから出てスクリーンに到達するまでといった過程において,波動として存在します.特に,2重スリットを通過するとき,1個の電子は,波動として2つのスリットを同時に通るように振る舞うのです.そうでないならば,1個の電子は干渉しようがありません.そして,スクリーンに到達して,はじめて1個の粒子として確認されます.
上記のように,電子がスクリーンのどの場所で観測できるかを決定することが不可能であるという事実は,干渉模様を示している粒子数の分布 ![]() が,粒子として存在する確率に比例することを意味します.そこで,
が,粒子として存在する確率に比例することを意味します.そこで,![]() を粒子1個の存在確率として定義し直し,
を粒子1個の存在確率として定義し直し,
と表します.![]() は存在確率密度です.つまり,
は存在確率密度です.つまり,
![]() は,時刻
は,時刻 ![]() ,座標
,座標 ![]() における微小1次元空間
における微小1次元空間 ![]() の中に,1個の粒子が観測される確率を表します.(無限小をとると,存在確率は
の中に,1個の粒子が観測される確率を表します.(無限小をとると,存在確率は
![]() となります.)また,1次元空間全体(スクリーン上)で粒子が存在する確率が
となります.)また,1次元空間全体(スクリーン上)で粒子が存在する確率が ![]() であるという規格化条件,
であるという規格化条件,
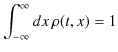
が成立します.(粒子は1次元空間全てにわたって存在する可能性があります.したがって,![]() から
から ![]() まで積分しました.)前のSectionで触れたように,ミクロ世界では決定論ではなく確率的性質が本質的な役割を果たします.ニュートンの力学的自然観の中心的概念である決定論的因果律を否定し,確率法則が支配する量子力学的自然観を打ち立てようとしているのです.アインシュタインは "神がサイコロをふるものか." と言い,量子力学が不完全な理論であると反論しましたが,現在において,多くの実験結果は量子力学が正しいことを立証しています.
まで積分しました.)前のSectionで触れたように,ミクロ世界では決定論ではなく確率的性質が本質的な役割を果たします.ニュートンの力学的自然観の中心的概念である決定論的因果律を否定し,確率法則が支配する量子力学的自然観を打ち立てようとしているのです.アインシュタインは "神がサイコロをふるものか." と言い,量子力学が不完全な理論であると反論しましたが,現在において,多くの実験結果は量子力学が正しいことを立証しています.
それでは,波動関数 ![]() と存在確率密度
と存在確率密度 ![]() の関係を考えましょう.一般に波動の強度(エネルギー)は,振幅の2乗と角振動数の2乗に比例します.ここで,一般に波動関数は,
の関係を考えましょう.一般に波動の強度(エネルギー)は,振幅の2乗と角振動数の2乗に比例します.ここで,一般に波動関数は,
と表すことができます.(![]() は振幅,
は振幅,
![]() は位相です.)このとき,
は位相です.)このとき,
となります.波動関数の強度は,上述したように振幅 ![]() の2乗に比例しますから,ということは,
の2乗に比例しますから,ということは,![]() の絶対値の2乗に比例することになりますね.以上のことから,存在確率密度
の絶対値の2乗に比例することになりますね.以上のことから,存在確率密度 ![]() は
は ![]() の絶対値の2乗に比例する,と仮定することができるでしょう.
の絶対値の2乗に比例する,と仮定することができるでしょう.
ここで,![]() は比例定数です.規格化条件より,
は比例定数です.規格化条件より,
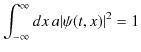
が成立します.![]() の定数倍も
の定数倍も ![]() と同じ性質の波動関数を表しますので,
と同じ性質の波動関数を表しますので,
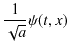
を改めて,![]() と置き直すと,
と置き直すと,
となります.このように,確率密度を与える量として,![]() を確率振幅と呼ぶことにします.ド・ブロイ波は波動関数で表されますが,その正体は複素数の確率の波動だったのです.この波動関数の確率解釈を唱えたのはボルンです.
を確率振幅と呼ぶことにします.ド・ブロイ波は波動関数で表されますが,その正体は複素数の確率の波動だったのです.この波動関数の確率解釈を唱えたのはボルンです.
"ド・ブロイ波→波動関数![]() (複素数)=確率振幅
(複素数)=確率振幅![]() (複素数)"
(複素数)"
概念の発展の繋がりを表記しました.
ここで,2重スリットの実験に戻りましょう.スリット ![]() から出た波動の確率振幅は
から出た波動の確率振幅は
![]() であり,スリット
であり,スリット ![]() から出た波動の確率振幅は
から出た波動の確率振幅は
![]() となります.もし,スリットの片方が閉じていれば干渉は起こりませんでした.スリット
となります.もし,スリットの片方が閉じていれば干渉は起こりませんでした.スリット ![]() が開いていて,スリット
が開いていて,スリット ![]() が閉じていれば,すなわち,存在確率密度分布は,
が閉じていれば,すなわち,存在確率密度分布は,
となります.スリット ![]() が開いていて,スリット
が開いていて,スリット ![]() が閉じていれば,すなわち,存在確率密度分布は,
が閉じていれば,すなわち,存在確率密度分布は,
となります.スリットが両方とも開いている場合は,存在確率密度分布
![]() は,
は,
![]() にはなりません.(存在確率密度分布は粒子数の分布と同じ干渉模様になりますね.)
にはなりません.(存在確率密度分布は粒子数の分布と同じ干渉模様になりますね.)
正しい関係式を見つけましょう.2つのスリットが開いているとき,電子の波動の一般量である確率振幅 ![]() は,重ね合わせの原理と呼ばれる波動一般について成立する関係によって合成されます.その内容は,2つの確率振幅が存在するときは,重ね合わされて,その和が合成された確率振幅になるというものです.
は,重ね合わせの原理と呼ばれる波動一般について成立する関係によって合成されます.その内容は,2つの確率振幅が存在するときは,重ね合わされて,その和が合成された確率振幅になるというものです.
2つの確率振幅は,同位相で2重スリットを通過するため,重ね合わせの原理に従い,合成され,スクリーン上で干渉を起こします.その理由は,水波,音波,光波といった波動一般の場合から類推されますが,ここでは,複素数の重ね合わせによる干渉になります.複素数である確率振幅は,
と表されますね.ここで,
![]() は位相でした.よって,スリットを両方とも開けた場合の,存在確率密度は次式で求められます.
は位相でした.よって,スリットを両方とも開けた場合の,存在確率密度は次式で求められます.
ここで,
![]() は
は ![]() の複素共役を表します.最後の式の第3項が干渉の効果を示しています.
の複素共役を表します.最後の式の第3項が干渉の効果を示しています.
スクリーンに到達して電子を観測したとき,それは紛れもなく粒子でした.スクリーンに到達するまで確率振幅をもつ波動として空間的に広がって存在していた電子が,スクリーン上で観測された瞬間に粒子になるのです.空間的に広がっていた波動が,観測した瞬間に1点に集まる,つまり局在することになります.これを量子飛躍といいます.(もっとも,スクリーンに到達する前の過程においても,観測を行えば量子飛躍が起こり,粒子が現れますが,いまはそういったことは行わないことにします.)このように,観測という行為は特別な意味を持っています.観測による波動関数の量子飛躍について,
と表しておきましょう.矢印の左側の波動関数 ![]() は,
は,![]() と
と ![]() の関数であり,時間的に変動し,空間的に広がっています.矢印の右側の波動関数は
の関数であり,時間的に変動し,空間的に広がっています.矢印の右側の波動関数は ![]() と記しましたが,これは時間的変化しない波動関数になったことを意味しています.(空間的にも局在します.)
と記しましたが,これは時間的変化しない波動関数になったことを意味しています.(空間的にも局在します.)![]() の右下の
の右下の ![]() は電子が局在する座標を表します.この量子飛躍の前後において因果関係はなく,観測される確率のみを波動関数,すなわち確率振幅から計算することができます.
は電子が局在する座標を表します.この量子飛躍の前後において因果関係はなく,観測される確率のみを波動関数,すなわち確率振幅から計算することができます.
波動関数(確率振幅)は,以上のように確率の波動という意味をもち,観測により量子飛躍する存在です.このような性質をもつ存在を,より抽象化して量子状態と名付けることにしましょう.波動関数並びに確率振幅は,波動力学における量子状態の表現形式なのです.概念の発展の繋がりを示しておきます.
"ド・ブロイ波→波動力学的状態(波動関数=確率振幅)→量子力学的状態(量子状態)"
7.3 量子状態ψについての3つの原理
前Sectionの重ね合わせの原理,
を拡張して一般化しましょう.シュレディンガー方程式を満たす,
の ![]() 個の
個の
![]() が存在するとき,
が存在するとき,
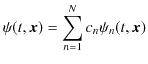
もシュレディンガー方程式を満たすという定理が成立します.(空間は3次元に拡張しました.
![]() です.)ここで,
です.)ここで,![]() は一般に複素数の定数です.この定理の証明にはシュレディンガー方程式の線形性を使います.
は一般に複素数の定数です.この定理の証明にはシュレディンガー方程式の線形性を使います.
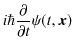 |
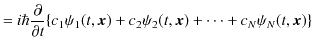 |
|
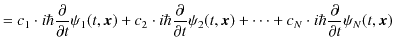 |
||
(証明終.)(![]() は無限大までとることができます.)この定理も重ね合わせの原理といいます.
は無限大までとることができます.)この定理も重ね合わせの原理といいます.
ここで,このChapterで見てきた原理をまとめておきます.ただし,空間は3次元に拡張しておきます.そして,空間についての3次元積分を,
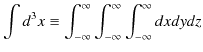
と表記することにします.かなり簡略化した表記方法ですが,これから何度も使いますので,このようにしておきます.積分範囲は,各成分について ![]() から
から![]() までとっていますが,これは粒子が存在する確率が全空間にあるためです.
までとっていますが,これは粒子が存在する確率が全空間にあるためです.
原理7.1(ボルンの確率解釈) "粒子の存在確率密度は,量子状態を表す規格化された確率振幅の絶対値の2乗で求められます.
この量を全空間にわたって積分したものは全確率 ![]() になります.
になります.
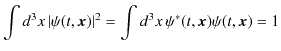
この式を規格化条件といいます."
原理7.2(重ね合わせの原理) "系の量子状態を表す波動関数,
がシュレディンガー方程式の解であるならば,重ね合わせた波動関数,
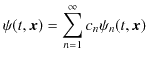
もシュレディンガー方程式の解になります."
原理7.3(観測による量子状態の量子飛躍) "波動として時間的に変動し,空間的に広がっている量子状態を表す
![]() は,観測という行為によって量子飛躍し,局在します.
は,観測という行為によって量子飛躍し,局在します.
その結果,粒子が観測されます.量子飛躍に因果関係はなく,ただ存在確率のみを知ることができます."
以上,3つの原理は波動力学の本質であり,古典的な概念とは相いれないものです.物質(電子)の2重性は解明されたのです.このSectionでまとめた3つの原理をもとに,量子力学を基礎付けている理論を,コペンハーゲン解釈といいます.その名前の由来は,量子力学の研究の中心となったニールス・ボーア研究所が,デンマークの首都コペンハーゲンにあることからきています.コペンハーゲン解釈は量子力学の正統的な理論です.
7.4 時間に依存しない量子状態φについて,3つの原理の変形
前Sectionの3つの原理は,時間に依存する波動関数
![]() についてのものでした.これらの原理を時間に依存しない波動関数
についてのものでした.これらの原理を時間に依存しない波動関数
![]() について,書き直しておきましょう.まず,規格化条件がどのようになるか,確認しておきます."シュレディンガー方程式" のChapterの最後の方で出てきた,
について,書き直しておきましょう.まず,規格化条件がどのようになるか,確認しておきます."シュレディンガー方程式" のChapterの最後の方で出てきた,
![]() と
と
![]() の間の関係式,
の間の関係式,
において,
![]() の定数倍も
の定数倍も
![]() と同じ量子状態を表すので,
と同じ量子状態を表すので,
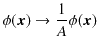
と置き直します.この場合,
が成立します.(この式が,
![]() と
と
![]() の間の一般的な関係式です.)これを,
の間の一般的な関係式です.)これを,
![]() についての規格化条件,
についての規格化条件,
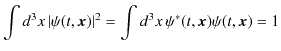
に代入し,
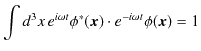
となります.故に,
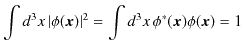
という
![]() についての規格化条件が得られました.したがって,
についての規格化条件が得られました.したがって,
![]() のときと同様に,
のときと同様に,
という量で,
![]() についての存在確率密度を与えることができます.
についての存在確率密度を与えることができます.
![]() について,
について,
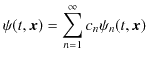
が時間に依存するシュレディンガー方程式の解であるという,重ね合わせの原理が成立しました.この関係を,
![]() を使って表しておきましょう.
を使って表しておきましょう.
![]() と
と
![]() の間の関係式,
の間の関係式,
より,(ここで,
![]() としておきます.)
としておきます.)
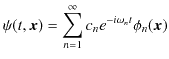
となります.ここで,
とおくと,
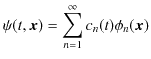
と,
![]() を無限個の
を無限個の
![]() によって展開して表すことができます.
によって展開して表すことができます.
観測による波動関数
![]() の量子飛躍,
の量子飛躍,
も書き直しておきます.すなわち,
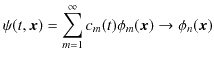
となります.波動関数
![]() は展開した
は展開した
![]() の中の1つに量子飛躍するのです.ここで,無限個の自然数
の中の1つに量子飛躍するのです.ここで,無限個の自然数 ![]() によって添え字が付けられた
によって添え字が付けられた
![]() の中の1つである,
の中の1つである,![]() 番目の
番目の
![]() に量子飛躍する場合を挙げました.実は
に量子飛躍する場合を挙げました.実は
![]() の添え字の付け方には連続した数を使うこともあります.例えば,連続量の座標
の添え字の付け方には連続した数を使うこともあります.例えば,連続量の座標 ![]() によって添え字を付けることもあります.これまでの議論の,電子をある座標
によって添え字を付けることもあります.これまでの議論の,電子をある座標 ![]() に観測するときの量子飛躍では,添え字
に観測するときの量子飛躍では,添え字 ![]() の代わりに添え字
の代わりに添え字 ![]() が使われています.
が使われています.
7.5 確率の保存と確率の流れ
ボルンの確率解釈が首尾一貫したものになるためには,規格化条件,
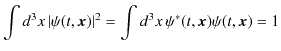
が,時間に依存しないものである必要があります.時間で微分して,確かめてみましょう.
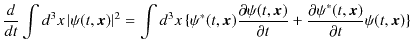
となります.ここで,シュレディンガー方程式,
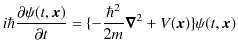
より,
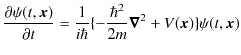
となります.この式の複素共役をとると,
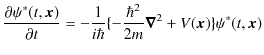
となります.ただし,ポテンシャル ![]() は実数と仮定しました.(
は実数と仮定しました.(
![]() )これらの式を代入して計算します.
)これらの式を代入して計算します.
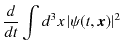 |
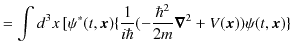 |
|
![$\displaystyle \,\,\,+\{-\dfrac{1}{i\hbar}(-\dfrac{\hbar^{2}}{2m}\bm{\nabla}^{2}+V(\bm{x}))\psi^{*}(t,\bm{x})\}\psi(t,\bm{x})]$](ja_Chapter7_QuantumState_WaveFunctionAndProbabilityAmplitude_images/img150.png) |
||
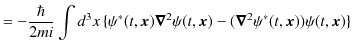 |
||
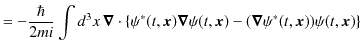 |
ここで,
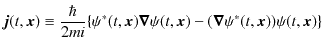
を定義し,ベクトル解析のガウスの定理,
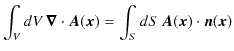
を使います.(左辺は体積分で,
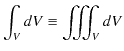
と積分記号は定義されます.また,
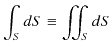
は面積分です.そして,
![]() は面積分する表面の単位法線ベクトルです.)
は面積分する表面の単位法線ベクトルです.)
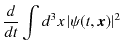 |
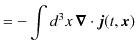 |
|
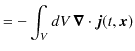 |
||
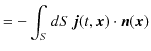 |
ここで,波束の場合,遠方で
![]() は 0 になるので,最後の表面積分は 0 になります.したがって,
は 0 になるので,最後の表面積分は 0 になります.したがって,
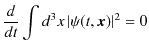 |
||
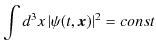 |
となります.
![]() に適当な定数を掛けて規格化すると,その規格化条件は常に成立することが保障されたことになります.
に適当な定数を掛けて規格化すると,その規格化条件は常に成立することが保障されたことになります.
上の議論を局所的な関係に書き直しておきましょう.存在確率密度,
を時間で偏微分します.
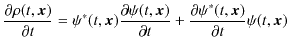
ここで,シュレディンガー方程式,
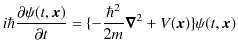
より,
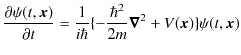
となります.この式の複素共役をとると,
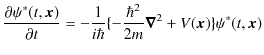
となります.ただし,ポテンシャル ![]() は実数と仮定しました.(
は実数と仮定しました.(
![]() )これらの式を代入して計算します.
)これらの式を代入して計算します.
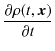 |
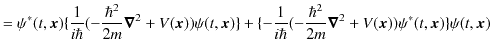 |
|
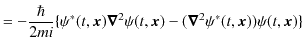 |
||
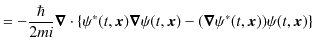 |
||
となります.したがって,
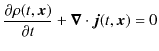
という関係式が成立します.この式は流体力学でお馴染みのものであり,湧き出しや吸い込みがない場合に,密度
![]() ,流れのベクトル
,流れのベクトル
![]() をもつ流体の保存則です.したがって,ベクトル
をもつ流体の保存則です.したがって,ベクトル
![]() を確率の流れ密度として,上式は確率の流れの保存則と考えることができます.
を確率の流れ密度として,上式は確率の流れの保存則と考えることができます.
このChapterでは,量子力学の基礎概念である量子状態について考えました.次のChapterでは,もう1つの基礎概念であるオブザーバブルについて見ていきましょう.